Marching Squares 2, sharing and crossing

Now that you have a basic marching-squares canvas, it's time to improve its capabilities. This time we'll cover vertex reuse and how to find edge intersections.

You'll learn to

This tutorial is the second in a series about Marching Squares.

This tutorial has been made with Unity 4.5.2. It might not work for older versions.

Free-form painting on a regular grid.

Reusing Vertices

When triangulating cells, we consider each cell in isolation. This keeps things simple, but results in quite a lot of vertices. For example, an isolated filled voxel results in four cells containing a single triangle, each with three vertices, for a total of twelve vertices.

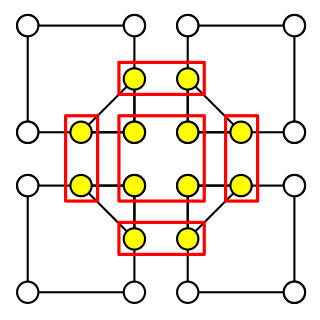
triangulation shared vertices
Made with twelve vertices, but only needs five.

In this example there are really only five unique vertices, but the central vertex is included four times while the others are included twice each. So if we could let adjacent cells share vertices, we would reduce the vertex count considerably.

To reuse vertices, we have to keep track of them. The most straightforward approach would be to store a vertex index per voxel, but we don't really have to remember that many at once. As we triangulate the grids one row of cells at a time, we can suffice with caching the vertex indices for one row of cells. While this is a bit more involved, it means our cache size is linear instead of quadratic, so it scales better.

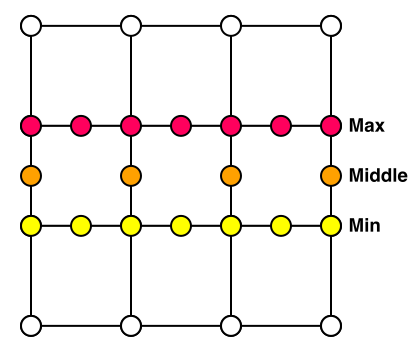
For a single row of cells, we need to keep track of two rows of vertex indices. These are the minimum and maximum vertex rows, or in our case the bottom and top rows. There is also a middle row, which is for all vertices along the vertical edges between cells of the row.

Rows of cached vertices.

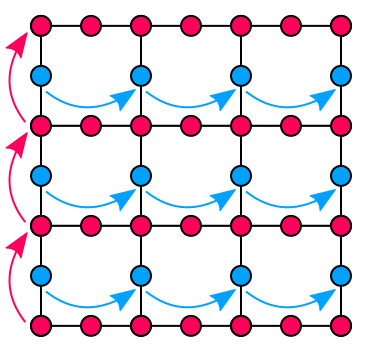
After completing a row of cells, the current maximum row becomes the minimum row for the next row of cells. This shifting works the same as the shifting of dummy voxels used to fill the gaps between grids.

Filling the Cache

Before filling the cache, we need to know its size. The minimum and maximum cache rows need room for one vertex index per voxel plus one for each X edge between those voxels. And vertices of the gap cell need to be cached too, which adds another two. So these caches have to be arrays with a length equal to twice the grid resolution plus one.

The middle row only needs room for one index per Y edge. Actually, as this part of the cache isn't needed for the next cell row, we don't need to remember the entire row. We can suffice by caching two indices and shifting those, as if they're two other minimum and maximum arrays of length one.

Progression through caches.

Now it's time to start coding again. Add two cache arrays and two cache integers to VoxelGrid and initialize the arrays in Awake.

	private int[] rowCacheMax, rowCacheMin;
	private int edgeCacheMin, edgeCacheMax;
	
	private void Awake () {
		…

		rowCacheMax = new int[resolution * 2 + 1];
		rowCacheMin = new int[resolution * 2 + 1];
		Refresh();
	}

When triangulating, we now have to fill the cache. To start the process, we have to fill the initial row.

	private void Triangulate () {
		vertices.Clear();
		triangles.Clear();
		mesh.Clear();

		if (xNeighbor != null) {
			dummyX.BecomeXDummyOf(xNeighbor.voxels[0], gridSize);
		}
		FillFirstRowCache();
		TriangulateCellRows();
		if (yNeighbor != null) {
			TriangulateGapRow();
		}

		mesh.vertices = vertices.ToArray();
		mesh.triangles = triangles.ToArray();
	}

The first step of the first row is to check if the first corner needs a vertex, and if so cache it.

	private void FillFirstRowCache () {
		CacheFirstCorner(voxels[0]);
	}

Caching the corner vertex means that we add it to the vertex list and store its index in our cache. As we're always working on the top row, we store it in the maximum cache row. Of course you should only add the vertex if the voxel is actually filled.

	private void CacheFirstCorner (Voxel voxel) {
		if (voxel.state) {
			rowCacheMax[0] = vertices.Count;
			vertices.Add(voxel.position);
		}
	}

To cache the rest of the row, we have to visited successive pairs of edges and corners. We create another method for that, and besides passing the voxels we also pass it the cache index. As we visit two additional vertices per cell, the cache index increases twice as fast as the cell index.

	private void FillFirstRowCache () {
		CacheFirstCorner(voxels[0]);
		for (int i = 0; i < resolution - 1; i++) {
			CacheNextEdgeAndCorner(i * 2, voxels[i], voxels[i + 1]);
		}
	}

The edge only has to be cached if the two corner voxels are different, because that's when there is an edge crossing. Then the next corner, which is the second corner of the current cell, is cached. 

	private void CacheNextEdgeAndCorner (int i, Voxel xMin, Voxel xMax) {
		if (xMin.state != xMax.state) {
			rowCacheMax[i + 1] = vertices.Count;
			vertices.Add(xMin.xEdgePosition);
		}
		if (xMax.state) {
			rowCacheMax[i + 2] = vertices.Count;
			vertices.Add(xMax.position);
		}
	}

After that we have to cache the vertices of the gap cell. Let's also move the dummy code into FillFirstCacheRow so its initialization and use are in the same place.

	private void Triangulate () {
		vertices.Clear();
		triangles.Clear();
		mesh.Clear();

		FillFirstRowCache();
		TriangulateCellRows();
		if (yNeighbor != null) {
			TriangulateGapRow();
		}

		mesh.vertices = vertices.ToArray();
		mesh.triangles = triangles.ToArray();
	}

	private void FillFirstRowCache () {
		CacheFirstCorner(voxels[0]);
		int i;
		for (i = 0; i < resolution - 1; i++) {
			CacheNextEdgeAndCorner(i * 2, voxels[i], voxels[i + 1]);
		}
		if (xNeighbor != null) {
			dummyX.BecomeXDummyOf(xNeighbor.voxels[0], gridSize);
			CacheNextEdgeAndCorner(i * 2, voxels[i], dummyX);
		}
	}

Now we continue with triangulating the cell rows. Each row, we begin by swapping the cache rows so the previous maximum becomes the new minimum.

	private void TriangulateCellRows () {
		int cells = resolution - 1;
		for (int i = 0, y = 0; y < cells; y++, i++) {
			SwapRowCaches();
			
			for (int x = 0; x < cells; x++, i++) {
				TriangulateCell(
					voxels[i],
					voxels[i + 1],
					voxels[i + resolution],
					voxels[i + resolution + 1]);
			}
			if (xNeighbor != null) {
				TriangulateGapCell(i);
			}
		}
	}

	private void SwapRowCaches () {
		int[] rowSwap = rowCacheMin;
		rowCacheMin = rowCacheMax;
		rowCacheMax = rowSwap;
	}

Each row, again start with the first corner and keep caching the next edge and corner. As we're working on the top vertices of the cells, we have to add the resolution to the current cell index.

	private void TriangulateCellRows () {
		int cells = resolution - 1;
		for (int i = 0, y = 0; y < cells; y++, i++) {
			SwapRowCaches();
			CacheFirstCorner(voxels[i + resolution]);

			for (int x = 0; x < cells; x++, i++) {
				CacheNextEdgeAndCorner(x * 2, voxels[i + resolution], voxels[i + resolution + 1]);
				TriangulateCell(
					voxels[i],
					voxels[i + 1],
					voxels[i + resolution],
					voxels[i + resolution + 1]);
			}
			if (xNeighbor != null) {
				TriangulateGapCell(i);
			}
		}
	}

Now we also have to cache the edge vertices of the middle row. We can use a single method for that which both shifts the cache and adds the vertex. This method needs to be called at the start of each row for the leftmost edge and once for the right edge of each cell. Because the same voxels will now be needed a couple of times in the inner loop, I put them in variables for clarity.

	private void TriangulateCellRows () {
		int cells = resolution - 1;
		for (int i = 0, y = 0; y < cells; y++, i++) {
			SwapRowCaches();
			CacheFirstCorner(voxels[i + resolution]);
			CacheNextMiddleEdge(voxels[i], voxels[i + resolution]);

			for (int x = 0; x < cells; x++, i++) {
				Voxel
					a = voxels[i],
					b = voxels[i + 1],
					c = voxels[i + resolution],
					d = voxels[i + resolution + 1];
				CacheNextEdgeAndCorner(x * 2, c, d);
				CacheNextMiddleEdge(b, d);
				TriangulateCell(a, b, c, d);
			}
			if (xNeighbor != null) {
				TriangulateGapCell(i);
			}
		}
	}
	
	private void CacheNextMiddleEdge (Voxel yMin, Voxel yMax) {
		edgeCacheMin = edgeCacheMax;
		if (yMin.state != yMax.state) {
			edgeCacheMax = vertices.Count;
			vertices.Add(yMin.yEdgePosition);
		}
	}

And the gap cell at the end of each rows needs caching too.

	private void TriangulateGapCell (int i) {
		Voxel dummySwap = dummyT;
		dummySwap.BecomeXDummyOf(xNeighbor.voxels[i + 1], gridSize);
		dummyT = dummyX;
		dummyX = dummySwap;
		CacheNextEdgeAndCorner((resolution - 1) * 2, voxels[i + resolution], dummyX);
		CacheNextMiddleEdge(dummyT, dummyX);
		TriangulateCell(voxels[i], dummyT, voxels[i + resolution], dummyX);
	}

The last step is to deal with the gap row at the top of each grid. The approach is the same, but with more dummies.

	private void TriangulateGapRow () {
		dummyY.BecomeYDummyOf(yNeighbor.voxels[0], gridSize);
		int cells = resolution - 1;
		int offset = cells * resolution;
		SwapRowCaches();
		CacheFirstCorner(dummyY);
		CacheNextMiddleEdge(voxels[cells * resolution], dummyY);

		for (int x = 0; x < cells; x++) {
			Voxel dummySwap = dummyT;
			dummySwap.BecomeYDummyOf(yNeighbor.voxels[x + 1], gridSize);
			dummyT = dummyY;
			dummyY = dummySwap;
			CacheNextEdgeAndCorner(x * 2, dummyT, dummyY);
			CacheNextMiddleEdge(voxels[x + offset + 1], dummyY);
			TriangulateCell(voxels[x + offset], voxels[x + offset + 1], dummyT, dummyY);
		}

		if (xNeighbor != null) {
			dummyT.BecomeXYDummyOf(xyNeighbor.voxels[0], gridSize);
			CacheNextEdgeAndCorner(cells * 2, dummyY, dummyT);
			CacheNextMiddleEdge(dummyX, dummyT);
			TriangulateCell(voxels[voxels.Length - 1], dummyX, dummyY, dummyT);
		}
	}

Using the Cache

Right now we're caching all vertices, but aren't actually using them yet. So we just end up with even more vertices. We need new versions of our polygon methods that use indices instead of vertices. They're the same as the old ones, except that the parameters are integers and they no longer add vertices to the vertex list themselves.

	private void AddTriangle (int a, int b, int c) {
		triangles.Add(a);
		triangles.Add(b);
		triangles.Add(c);
	}

	private void AddQuad (int a, int b, int c, int d) {
		triangles.Add(a);
		triangles.Add(b);
		triangles.Add(c);
		triangles.Add(a);
		triangles.Add(c);
		triangles.Add(d);
	}

	private void AddPentagon (int a, int b, int c, int d, int e) {
		triangles.Add(a);
		triangles.Add(b);
		triangles.Add(c);
		triangles.Add(a);
		triangles.Add(c);
		triangles.Add(d);
		triangles.Add(a);
		triangles.Add(d);
		triangles.Add(e);
	}

To retrieve the cached vertices, we need to pass along the cache index to TriangulateCell, so give it another parameter.

	private void TriangulateCell (int i, Voxel a, Voxel b, Voxel c, Voxel d) {
		…
	}

We already calculated the cache index while processing the cells, so if we remember it we can simply pass it to TriangulateCell as well.

	private void TriangulateCellRows () {
		…
				int cacheIndex = x * 2;
				CacheNextEdgeAndCorner(cacheIndex, c, d);
				CacheNextMiddleEdge(b, d);
				TriangulateCell(cacheIndex, a, b, c, d);
		…
	}
	
	private void TriangulateGapCell (int i) {
		…
		int cacheIndex = (resolution - 1) * 2;
		CacheNextEdgeAndCorner(cacheIndex, voxels[i + resolution], dummyX);
		CacheNextMiddleEdge(dummyT, dummyX);
		TriangulateCell(cacheIndex, voxels[i], dummyT, voxels[i + resolution], dummyX);
	}
	
	private void TriangulateGapRow () {
		…

		for (int x = 0; x < cells; x++) {
			…
			int cacheIndex = x * 2;
			CacheNextEdgeAndCorner(cacheIndex, dummyT, dummyY);
			CacheNextMiddleEdge(voxels[x + offset + 1], dummyY);
			TriangulateCell(cacheIndex, voxels[x + offset], voxels[x + offset + 1], dummyT, dummyY);
		}

		if (xNeighbor != null) {
			dummyT.BecomeXYDummyOf(xyNeighbor.voxels[0], gridSize);
			int cacheIndex = cells * 2;
			CacheNextEdgeAndCorner(cacheIndex, dummyY, dummyT);
			CacheNextMiddleEdge(dummyX, dummyT);
			TriangulateCell(cacheIndex, voxels[voxels.Length - 1], dummyX, dummyY, dummyT);
		}
	}

Now we have to update the switch statement in TriangulateCell. Each vertex argument has to be replaced with the corresponding cache entry. Here is the complete mapping.

a.positionbecomesrowCacheMin[i]
a.xEdgePositionbecomesrowCacheMin[i + 1]
b.positionbecomesrowCacheMin[i + 2]
c.positionbecomesrowCacheMax[i]
c.xEdgePositionbecomesrowCacheMax[i + 1]
d.positionbecomesrowCacheMax[i + 2]
a.yEdgePositionbecomesedgeCacheMin
b.yEdgePositionbecomesedgeCacheMax
	private void TriangulateCell (int i, Voxel a, Voxel b, Voxel c, Voxel d) {
		int cellType = 0;
		if (a.state) {
			cellType |= 1;
		}
		if (b.state) {
			cellType |= 2;
		}
		if (c.state) {
			cellType |= 4;
		}
		if (d.state) {
			cellType |= 8;
		}
		switch (cellType) {
		case 0:
			return;
		case 1:
			AddTriangle(rowCacheMin[i], edgeCacheMin, rowCacheMin[i + 1]);
			break;
		case 2:
			AddTriangle(rowCacheMin[i + 2], rowCacheMin[i + 1], edgeCacheMax);
			break;
		case 3:
			AddQuad(rowCacheMin[i], edgeCacheMin, edgeCacheMax, rowCacheMin[i + 2]);
			break;
		case 4:
			AddTriangle(rowCacheMax[i], rowCacheMax[i + 1], edgeCacheMin);
			break;
		case 5:
			AddQuad(rowCacheMin[i], rowCacheMax[i], rowCacheMax[i + 1], rowCacheMin[i + 1]);
			break;
		case 6:
			AddTriangle(rowCacheMin[i + 2], rowCacheMin[i + 1], edgeCacheMax);
			AddTriangle(rowCacheMax[i], rowCacheMax[i + 1], edgeCacheMin);
			break;
		case 7:
			AddPentagon(
				rowCacheMin[i], rowCacheMax[i], rowCacheMax[i + 1], edgeCacheMax, rowCacheMin[i + 2]);
			break;
		case 8:
			AddTriangle(rowCacheMax[i + 2], edgeCacheMax, rowCacheMax[i + 1]);
			break;
		case 9:
			AddTriangle(rowCacheMin[i], edgeCacheMin, rowCacheMin[i + 1]);
			AddTriangle(rowCacheMax[i + 2], edgeCacheMax, rowCacheMax[i + 1]);
			break;
		case 10:
			AddQuad(rowCacheMin[i + 1], rowCacheMax[i + 1], rowCacheMax[i + 2], rowCacheMin[i + 2]);
			break;
		case 11:
			AddPentagon(
			    rowCacheMin[i + 2], rowCacheMin[i], edgeCacheMin, rowCacheMax[i + 1], rowCacheMax[i + 2]);
			break;
		case 12:
			AddQuad(edgeCacheMin, rowCacheMax[i], rowCacheMax[i + 2], edgeCacheMax);
			break;
		case 13:
			AddPentagon(
				rowCacheMax[i], rowCacheMax[i + 2], edgeCacheMax, rowCacheMin[i + 1], rowCacheMin[i]);
			break;
		case 14:
			AddPentagon(
				rowCacheMax[i + 2],rowCacheMin[i + 2], rowCacheMin[i + 1], edgeCacheMin, rowCacheMax[i]);
			break;
		case 15:
			AddQuad(rowCacheMin[i], rowCacheMax[i], rowCacheMax[i + 2], rowCacheMin[i + 2]);
			break;
		}
	}

That should do it, your meshes should now contain considerably less vertices! You can now also get rid of the old polygon methods that have vertex parameters.

Reducing Edge Data

Our new approach also allows for another simplification and optimization of Voxel. We used to store edge crossing as vectors, because that way we could directly pass them into our polygon methods. As we no longer do that, we can get rid of the redundant coordinates, storing only two edge floats per vertex instead of four.

	public Vector2 position;

	public float xEdge, yEdge;
	
	public Voxel (int x, int y, float size) {
		position.x = (x + 0.5f) * size;
		position.y = (y + 0.5f) * size;

		xEdge = position.x + size * 0.5f;
		yEdge = position.y + size * 0.5f;
	}

	public Voxel () {}

	public void BecomeXDummyOf (Voxel voxel, float offset) {
		state = voxel.state;
		position = voxel.position;
		position.x += offset;
		xEdge = voxel.xEdge + offset;
		yEdge = voxel.yEdge;
	}

	public void BecomeYDummyOf (Voxel voxel, float offset) {
		state = voxel.state;
		position = voxel.position;
		position.y += offset;
		xEdge = voxel.xEdge;
		yEdge = voxel.yEdge + offset;
	}

	public void BecomeXYDummyOf (Voxel voxel, float offset) {
		state = voxel.state;
		position = voxel.position;
		position.x += offset;
		position.y += offset;
		xEdge = voxel.xEdge + offset;
		yEdge = voxel.yEdge + offset;
	}

The only places where VoxelGrid needs the edge positions are in CacheNextEdgeAndCorner and CacheNextMiddleEdge. We have to update these methods so they construct the edge vertices when needed, retrieving the missing coordinate from the voxel's position.

	private void CacheNextEdgeAndCorner (int i, Voxel xMin, Voxel xMax) {
		if (xMin.state != xMax.state) {
			rowCacheMax[i + 1] = vertices.Count;
			Vector3 p;
			p.x = xMin.xEdge;
			p.y = xMin.position.y;
			p.z = 0f;
			vertices.Add(p);
		}
		if (xMax.state) {
			rowCacheMax[i + 2] = vertices.Count;
			vertices.Add(xMax.position);
		}
	}
	
	private void CacheNextMiddleEdge (Voxel yMin, Voxel yMax) {
		edgeCacheMin = edgeCacheMax;
		if (yMin.state != yMax.state) {
			edgeCacheMax = vertices.Count;
			Vector3 p;
			p.x = yMin.position.x;
			p.y = yMin.yEdge;
			p.z = 0f;
			vertices.Add(p);
		}
	}

Finding Edge Crossings

The previous section was useful, but didn't result in any visual change. This section is different, we're going to work on edge crossings.

Until now we've fixed edge crossings to the midpoint between voxels, which produces very rigid visuals. It's time we loosen up and calculate the actual edge intersections. But first, let's visualize our stencils so we can better see what we're editing.

Visualizing Stencils

To show the stencils we need objects. Create a default cube for the square stencil and a default cylinder for the circle stencil. The cylinder needs to be rotated 90 degrees around the X axis so it looks like a circle from our point of view. Remove the colliders from both of them, so they don't interfere with the input detection.

Give them some semitransparent material so you can both see the stencil shape and the grid while painting. I made a new Stencil material with the default Transparent / Diffuse shader and a red color with alpha set to 127.

Make them children of Voxel Map and deactivate them so they're not visible. Then add a public Transform array to VoxelMap and assign the shapes to them so they match the stencil options.

	public Transform[] stencilVisualizations;
Stencil Visualization objects.

We should show the visualization of the current stencil whenever the cursor hovers over the map, not only when drawing. To support this, swap and combine the if-statements in VoxelMap.Update and activate or deactivate the visualization as needed.

	private void Update () {
		Transform visualization = stencilVisualizations[stencilIndex];
		RaycastHit hitInfo;
		if (Physics.Raycast(Camera.main.ScreenPointToRay(Input.mousePosition), out hitInfo) &&
		    hitInfo.collider.gameObject == gameObject) {
			if (Input.GetMouseButton(0)) {
				EditVoxels(transform.InverseTransformPoint(hitInfo.point));
			}
			visualization.gameObject.SetActive(true);
		}
		else {
			visualization.gameObject.SetActive(false);
		}
	}
Centered visualization when hovering.

To correctly position and scale the visualization, we have perform the same calculations as in EditVoxels, so add those in. Because the calculation uses the bottom-left of the grid as its local origin, we have to undo this offset after figuring out the voxel's position.

			Vector2 center = transform.InverseTransformPoint(hitInfo.point);
			center.x += halfSize;
			center.y += halfSize;
			center.x = ((int)(center.x / voxelSize) + 0.5f) * voxelSize;
			center.y = ((int)(center.y / voxelSize) + 0.5f) * voxelSize;

			if (Input.GetMouseButton(0)) {
				EditVoxels(transform.InverseTransformPoint(hitInfo.point));
			}

			center.x -= halfSize;
			center.y -= halfSize;
			visualization.localPosition = center;
			visualization.localScale = Vector3.one * ((radiusIndex + 0.5f) * voxelSize * 2f);
			visualization.gameObject.SetActive(true);
Positioned and scaled.

Going off the Grid

Now we can see the stencil and can confirm that only the voxels inside its shape are affected. The next step is to no longer snap the stencil to exact voxel positions when editing. Because you might actually want to snap, let's make this optional. Add a configuration option and only snap the stencil's position when this is desired.

	public bool snapToGrid;
		
	private void Update () {
		…
			center.x += halfSize;
			center.y += halfSize;
			if (snapToGrid) {
				center.x = ((int)(center.x / voxelSize) + 0.5f) * voxelSize;
				center.y = ((int)(center.y / voxelSize) + 0.5f) * voxelSize;
			}

			if (Input.GetMouseButton(0)) {
				EditVoxels(transform.InverseTransformPoint(hitInfo.point));
			}
		…
	}
snap to grid no snapping
To snap or not.

Of course right now this only affects the stencil's visualization. To support this option for editing, VoxelStencil needs to work with actual positions instead of voxel coordinates. This means that we have to replace its integers with floats.

	protected float centerX, centerY, radius;

	public float XStart {
		get {
			return centerX - radius;
		}
	}
	
	public float XEnd {
		get {
			return centerX + radius;
		}
	}
	
	public float YStart {
		get {
			return centerY - radius;
		}
	}
	
	public float YEnd {
		get {
			return centerY + radius;
		}
	}

	public virtual void Initialize (bool fillType, float radius) {
		this.fillType = fillType;
		this.radius = radius;
	}

	public virtual void SetCenter (float x, float y) {
		centerX = x;
		centerY = y;
	}

Its Apply method now also needs to work with the actual position of a voxel. Let's adjust it so you provide it with a voxel which it directly edits, instead of returning the new voxel state. To make sure the voxel lies inside the square area, we now have to check whether the voxel's position lies within the stencil bounds.

	public virtual void Apply (Voxel voxel) {
		Vector2 p = voxel.position;
		if (p.x >= XStart && p.x <= XEnd && p.y >= YStart && p.y <= YEnd) {
			voxel.state = fillType;
		}
	}

And VoxelStencilCirle needs to be adjusted as well. This stencil already performed an explicit bounds check, it just needs to use floats now.

	private float sqrRadius;
	
	public override void Initialize (bool fillType, float radius) {
		base.Initialize (fillType, radius);
		sqrRadius = radius * radius;
	}
	
	public override void Apply (Voxel voxel) {
		float x = voxel.position.x - centerX;
		float y = voxel.position.y - centerY;
		if (x * x + y * y <= sqrRadius) {
			voxel.state = fillType;
		}
	}

Now let's change EditVoxels so it uses the center that we already calculated in Update. We used to add a one-voxel padding in the negative directions to make sure that gaps were updated property. As we now also have to make sure that edge crossings are updated at the edge of the stencil area, we have to add padding in the positive directions as well. Also note that we no longer need to worry about a voxel offset in the loops when updating the stencil center.

	private void Update () {
		…
			if (Input.GetMouseButton(0)) {
				EditVoxels(center);
			}
		…
	}

	private void EditVoxels (Vector2 center) {
		VoxelStencil activeStencil = stencils[stencilIndex];
		activeStencil.Initialize(fillTypeIndex == 0, (radiusIndex + 0.5f) * voxelSize);
		activeStencil.SetCenter(center.x, center.y);

		int xStart = (int)((activeStencil.XStart - voxelSize) / chunkSize);
		if (xStart < 0) {
			xStart = 0;
		}
		int xEnd = (int)((activeStencil.XEnd + voxelSize) / chunkSize);
		if (xEnd >= chunkResolution) {
			xEnd = chunkResolution - 1;
		}
		int yStart = (int)((activeStencil.YStart - voxelSize) / chunkSize);
		if (yStart < 0) {
			yStart = 0;
		}
		int yEnd = (int)((activeStencil.YEnd + voxelSize) / chunkSize);
		if (yEnd >= chunkResolution) {
			yEnd = chunkResolution - 1;
		}

		for (int y = yEnd; y >= yStart; y--) {
			int i = y * chunkResolution + xEnd;
			for (int x = xEnd; x >= xStart; x--, i--) {
				activeStencil.SetCenter(center.x - x * chunkSize, center.y - y * chunkSize);
				chunks[i].Apply(activeStencil);
			}
		}
	}

The final change is to VoxelGrid.Apply, which needs to figure out which voxels are covered.

	public void Apply (VoxelStencil stencil) {
		int xStart = (int)(stencil.XStart / voxelSize);
		if (xStart < 0) {
			xStart = 0;
		}
		int xEnd = (int)(stencil.XEnd / voxelSize);
		if (xEnd >= resolution) {
			xEnd = resolution - 1;
		}
		int yStart = (int)(stencil.YStart / voxelSize);
		if (yStart < 0) {
			yStart = 0;
		}
		int yEnd = (int)(stencil.YEnd / voxelSize);
		if (yEnd >= resolution) {
			yEnd = resolution - 1;
		}

		for (int y = yStart; y <= yEnd; y++) {
			int i = y * resolution + xStart;
			for (int x = xStart; x <= xEnd; x++, i++) {
				stencil.Apply(voxels[i]);
			}
		}
		Refresh();
	}
Free editing.

Finding Edge Crossings

Now we can edit without snapping, which results in new patterns, but it still doesn't look much like the stencil visualization. So now we're going to figure out exact edge crossings. We'll do this one step at a time.

Add a method to VoxelStencil to compute the horizontal crossing between two voxels. First check whether the voxels are different, which means that there is a crossing. If so, try to find it.

	public void SetHorizontalCrossing (Voxel xMin, Voxel xMax) {
		if (xMin.state != xMax.state) {
			FindHorizontalCrossing(xMin, xMax);
		}
	}

How to calculate the exact intersection point depends on the stencil, so let's use a virtual method. As the basic stencil is a square, first check whether edge is inside the vertical bounds of the square. If not, the horizontal crossing isn't caused by this application of the stencil, it was already there.

	protected virtual void FindHorizontalCrossing (Voxel xMin, Voxel xMax) {
		if (xMin.position.y < YStart || xMin.position.y > YEnd) {
			return;
		}
	}
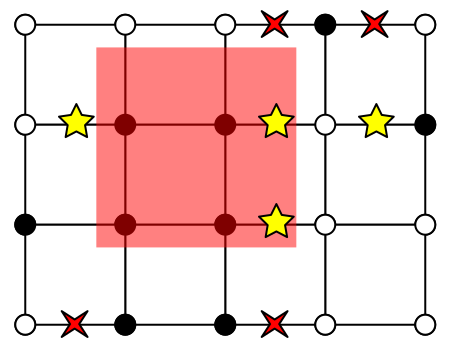
Eliminating horizontal crossings outside the vertical bounds.

Now we need to check which of the two voxels might lie inside the stencil's area. First consider the case of the left voxel matching our fill type. This means that the edge might cross the right side of the stencil. We should actually check this, because it could also be an old crossing that lies somewhere to the right or left of our stencil. If we're sure that it's actually passing through our stencil's border, we can set its exact position.

		if (xMin.position.y < YStart || xMin.position.y > YEnd) {
			return;
		}
		if (xMin.state == fillType) {
			if (xMin.position.x <= XEnd && xMax.position.x >= XEnd) {
				xMin.xEdge = XEnd;
			}
		}

We have to consider a possible crossing on the left side the of the stencil as well.

		if (xMin.state == fillType) {
			if (xMin.position.x <= XEnd && xMax.position.x >= XEnd) {
				xMin.xEdge = XEnd;
			}
		}
		else if (xMax.state == fillType) {
			if (xMin.position.x <= XStart && xMax.position.x >= XStart) {
				xMin.xEdge = XStart;
			}
		}
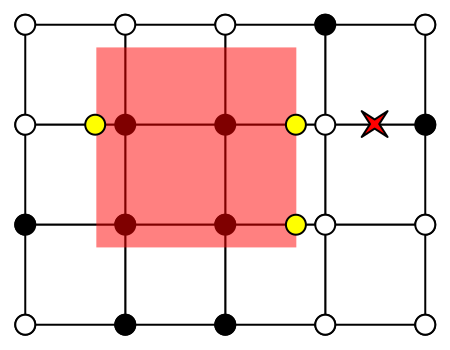
Finding actual horizontal crossings.

Next, do the same for vertical edge crossing.

	public void SetVerticalCrossing (Voxel yMin, Voxel yMax) {
		if (yMin.state != yMax.state) {
			FindVerticalCrossing(yMin, yMax);
		}
	}
	
	protected virtual void FindVerticalCrossing (Voxel yMin, Voxel yMax) {
		if (yMin.position.x < XStart || yMin.position.x > XEnd) {
			return;
		}
		if (yMin.state == fillType) {
			if (yMin.position.y <= YEnd && yMax.position.y >= YEnd) {
				yMin.yEdge = YEnd;
			}
		}
		else if (yMax.state == fillType) {
			if (yMin.position.y <= YStart && yMax.position.y >= YStart) {
				yMin.yEdge = YStart;
			}
		}
	}

Now VoxelGrid needs to actually set the edge crossing. This needs to be done after the stencil has been applied to the voxels.

	public void Apply (VoxelStencil stencil) {
		…

		for (int y = yStart; y <= yEnd; y++) {
			int i = y * resolution + xStart;
			for (int x = xStart; x <= xEnd; x++, i++) {
				stencil.Apply(voxels[i]);
			}
		}
		SetCrossings(stencil, xStart, xEnd, yStart, yEnd);
		Refresh();
	}

We need to increase the calculated voxel area by one step in each direction to cover all potential edges. Also check whether we need to pass gaps and if we have to cover the last vertical row, because all these cases require special attention.

	private void SetCrossings (VoxelStencil stencil, int xStart, int xEnd, int yStart, int yEnd) {
		bool crossHorizontalGap = false;
		bool lastVerticalRow = false;
		bool crossVerticalGap = false;

		if (xStart > 0) {
			xStart -= 1;
		}
		if (xEnd == resolution - 1) {
			xEnd -= 1;
			crossHorizontalGap = xNeighbor != null;
		}
		if (yStart > 0) {
			yStart -= 1;
		}
		if (yEnd == resolution - 1) {
			yEnd -= 1;
			lastVerticalRow = true;
			crossVerticalGap = yNeighbor != null;
		}
	}

Then loop over all cells, setting their bottom horizontal edges.

		Voxel a, b;
		for (int y = yStart; y <= yEnd; y++) {
			int i = y * resolution + xStart;
			b = voxels[i];
			for (int x = xStart; x <= xEnd; x++, i++) {
				a = b;
				b = voxels[i + 1];
				stencil.SetHorizontalCrossing(a, b);
			}
		}

Check the left vertical edges as well, and the vertical rightmost edge at the end of each row.

		for (int y = yStart; y <= yEnd; y++) {
			int i = y * resolution + xStart;
			b = voxels[i];
			for (int x = xStart; x <= xEnd; x++, i++) {
				a = b;
				b = voxels[i + 1];
				stencil.SetHorizontalCrossing(a, b);
				stencil.SetVerticalCrossing(a, voxels[i + resolution]);
			}
			stencil.SetVerticalCrossing(b, voxels[i + resolution]);
		}

We need to visit the bottom horizontal edge of gaps cells as well.

		for (int y = yStart; y <= yEnd; y++) {
			int i = y * resolution + xStart;
			b = voxels[i];
			for (int x = xStart; x <= xEnd; x++, i++) {
				a = b;
				b = voxels[i + 1];
				stencil.SetHorizontalCrossing(a, b);
				stencil.SetVerticalCrossing(a, voxels[i + resolution]);
			}
			stencil.SetVerticalCrossing(b, voxels[i + resolution]);
			if (crossHorizontalGap) {
				dummyX.BecomeXDummyOf(xNeighbor.voxels[y * resolution], gridSize);
				stencil.SetHorizontalCrossing(b, dummyX);
			}
		}

And finally we have to do the same for the last vertical row, using a dummy to cross the vertical gap is there's a neighbor.

		if (includeLastVerticalRow) {
			int i = voxels.Length - resolution + xStart;
			b = voxels[i];
			for (int x = xStart; x <= xEnd; x++, i++) {
				a = b;
				b = voxels[i + 1];
				stencil.SetHorizontalCrossing(a, b);
				if (crossVerticalGap) {
					dummyY.BecomeYDummyOf(yNeighbor.voxels[x], gridSize);
					stencil.SetVerticalCrossing(a, dummyY);
				}
			}
			if (crossVerticalGap) {
				dummyY.BecomeYDummyOf(yNeighbor.voxels[xEnd + 1], gridSize);
				stencil.SetVerticalCrossing(b, dummyY);
			}
			if (crossHorizontalGap) {
				dummyX.BecomeXDummyOf(xNeighbor.voxels[voxels.Length - resolution], gridSize);
				stencil.SetHorizontalCrossing(b, dummyX);
			}
		}
already more like painting exact square crossings
Free crossings.

Keeping Crossings in Place

Now we get exact edge crossing, at least when using the square stencil. But you'll notice that edge positions are always replaced when painting. It looks like the contour is pulled toward the stencil, which is not intuitive. It makes more sense to only adjust edge positions when doing so would increase the covered area, not when it would reduce it. To do so, we need to compare the new edge position to the previous one.

Only set crossings that lie outside the old shape.

Comparing with the current edge position only makes sense if there actually was an edge crossing. So we need some way to indicate that there is no old edge data. As local positions are always positive inside a voxel grid, we could use a negative value for this purpose. We should make sure the number stays negative even when offset by a dummy. Using the minimum possible value for a float takes care of that.

As we start without edge crossings, each Voxel should initially have negative edge data.

	public Voxel (int x, int y, float size) {
		position.x = (x + 0.5f) * size;
		position.y = (y + 0.5f) * size;

		xEdge = float.MinValue;
		yEdge = float.MinValue;
	}

As VoxelStencil knows how to figure out edge crossings, give it the responsibility of erasing old edge data when it finds that there's no crossing.

	public void SetHorizontalCrossing (Voxel xMin, Voxel xMax) {
		if (xMin.state != xMax.state) {
			FindHorizontalCrossing(xMin, xMax);
		}
		else {
			xMin.xEdge = float.MinValue;
		}
	}

	public void SetVerticalCrossing (Voxel yMin, Voxel yMax) {
		if (yMin.state != yMax.state) {
			FindVerticalCrossing(yMin, yMax);
		}
		else {
			yMin.yEdge = float.MinValue;
		}
	}

Then it can check whether there's old edge data and if that should be replaced, before actually storing the new position.

	protected virtual void FindHorizontalCrossing (Voxel xMin, Voxel xMax) {
		if (xMin.position.y < YStart || xMin.position.y > YEnd) {
			return;
		}
		if (xMin.state == fillType) {
			if (xMin.position.x <= XEnd && xMax.position.x >= XEnd) {
				if (xMin.xEdge == float.MinValue || xMin.xEdge < XEnd) {
					xMin.xEdge = XEnd;
				}
			}
		}
		else if (xMax.state == fillType) {
			if (xMin.position.x <= XStart && xMax.position.x >= XStart) {
				if (xMin.xEdge == float.MinValue || xMin.xEdge > XStart) {
					xMin.xEdge = XStart;
				}
			}
		}
	}
	
	protected virtual void FindVerticalCrossing (Voxel yMin, Voxel yMax) {
		if (yMin.position.x < XStart || yMin.position.x > XEnd) {
			return;
		}
		if (yMin.state == fillType) {
			if (yMin.position.y <= YEnd && yMax.position.y >= YEnd) {
				if (yMin.yEdge == float.MinValue || yMin.yEdge < YEnd) {
					yMin.yEdge = YEnd;
				}
			}
		}
		else if (yMax.state == fillType) {
			if (yMin.position.y <= YStart && yMax.position.y >= YStart) {
				if (yMin.yEdge == float.MinValue || yMin.yEdge > YStart) {
					yMin.yEdge = YStart;
				}
			}
		}
	}
Growing only, like paint.

Completing the Circle

Finally, VoxelStencilCircle needs its own crossing logic, otherwise it produces nonsensical edges. That means we have to compute the intersection of a line and a circle, which fortunately is easy because we're working with strictly horizontal and vertical lines. First consider the horizontal right side.

	protected override void FindHorizontalCrossing (Voxel xMin, Voxel xMax) {
		float y2 = xMin.position.y - centerY;
		y2 *= y2;
		if (xMin.state == fillType) {
			float x = xMin.position.x - centerX;
			if (x * x + y2 <= sqrRadius) {
				x = centerX + Mathf.Sqrt(sqrRadius - y2);
				if (xMin.xEdge == float.MinValue || xMin.xEdge < x) {
					xMin.xEdge = x;
				}
			}
		}
	}

Then the horizontal left side.

		float y2 = xMin.position.y - centerY;
		y2 *= y2;
		if (xMin.state == fillType) {
			float x = xMin.position.x - centerX;
			if (x * x + y2 <= sqrRadius) {
				x = centerX + Mathf.Sqrt(sqrRadius - y2);
				if (xMin.xEdge == float.MinValue || xMin.xEdge < x) {
					xMin.xEdge = x;
				}
			}
		}
		else if (xMax.state == fillType) {
			float x = xMax.position.x - centerX;
			if (x * x + y2 <= sqrRadius) {
				x = centerX - Mathf.Sqrt(sqrRadius - y2);
				if (xMin.xEdge == float.MinValue || xMin.xEdge > x) {
					xMin.xEdge = x;
				}
			}
		}

And once again the same approach for vertical edges.

	protected override void FindVerticalCrossing (Voxel yMin, Voxel yMax) {
		float x2 = yMin.position.x - centerX;
		x2 *= x2;
		if (yMin.state == fillType) {
			float y = yMin.position.y - centerY;
			if (y * y + x2 <= sqrRadius) {
				y = centerY + Mathf.Sqrt(sqrRadius - x2);
				if (yMin.yEdge == float.MinValue || yMin.yEdge < y) {
					yMin.yEdge = y;
				}
			}
		}
		else if (yMax.state == fillType) {
			float y = yMax.position.y - centerY;
			if (y * y + x2 <= sqrRadius) {
				y = centerY - Mathf.Sqrt(sqrRadius - x2);
				if (yMin.yEdge == float.MinValue || yMin.yEdge > y) {
					yMin.yEdge = y;
				}
			}
		}
	}
Much better circles.

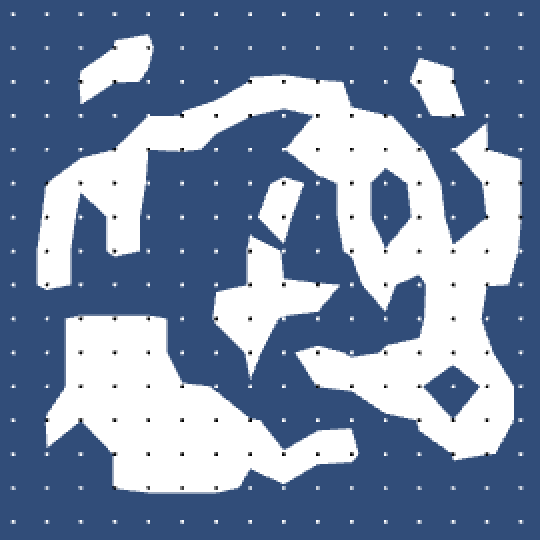
Our circle stencil finally produces something that looks like a circle! Of course a larger radius results in a better approximation, as that covers more voxels and edges. Unfortunately squares still don't have sharp corners, but we'll take care of that in the next tutorial.

Enjoyed the tutorial? Help me make more by becoming a patron!

Downloads

marching-squares-2-01.unitypackage
The project after Reusing Vertices.
marching-squares-2-finished.unitypackage
The finished project.
Is sharing vertices worth it?

The theoretical worst cases would be if either the grid is empty or only the four corner voxels of the grid were filled. In those cases there is no vertex reduction at all, but they have only zero and twelve vertices in total anyway.

A nontrivial bad case is a grid with lots of isolated filled voxels. A voxel on the edge of the grid still has no reduction, but there will be at most four of those. Isolated voxels along the grid edge can be reduced from six to four vertices, which is a 33% reduction. If the voxel doesn't touch the edge it goes from twelve to five vertices, which is a 58% reduction. 33% is already a significant reduction, and as there are typically more internal than edge voxels in a grid we can expect the final savings to be around 50%, which is very good.

If we start considering clumps of filled voxels the results get even better. An isolated 3x3 block of filled voxels that doesn't touch the grid edge has twelve edge vertices and nine voxel vertices, a total of 21. Without sharing we would end up with 60 vertices, so the reduction is 65%. A 5x5 block is reduced from 140 to 45 vertices, which is 67%.

So let's use a conservative estimate that vertex reuse cuts the amount of vertices in half, which benefits both memory, the CPU, and the GPU. This is quite significant, especially as we don't have to store much extra data to make it possible.

How does the cache scale better?

As the voxel grids are two-dimensional, their size is equal to the voxel resolution squared. Hence, they scale quadratically with the voxel resolution. That's why you cannot use a very high resolution. If we were to cache all vertices at once, the cache would also scale quadratically with the voxel resolution.

Deciding to only cache enough data to work on one cell row at a time allows us to use a one-dimensional cache, hence it scales linearly. As the voxel resolution increases, the cache size will quickly become insignificant compared to the voxel data.

Need we store the caches per grid?

No, it is not needed to give each grid its own cache data. You could get away with storing the caches once as static data. This would no longer make the cache scale with the amount of grids, making its size practically a non-issue.

I didn't bother with this optimization because it's not needed at the scale of this tutorial. To properly do it, you'd have to ensure that the shared cache is large enough to support the largest grid size that you're using, in case you have multiple voxels maps with different grid resolutions. Besides that, a shared cache wouldn't work if you were to use multi-threading to triangulate multiple grids at the same time. It might seem like overkill to worry about those cases, but they're good examples of things that will cause obscure bugs in some future version of your program.

How much space does this save?

As we remove two floats from the object, the short answer is that this optimization saves 8 bytes per voxel. But that doesn't say much if we don't know the total size of the object. Unfortunately the memory layout of an object is up to the compiler and depends on whether compiling for 32-bit or 64-bit systems. To get a general idea of size, let's assume we're building for 32-bit. In that case we start with 8 bytes for the object header. The three vectors add 24 bytes and the boolean adds another byte, so that's a total of 33 bytes. However, we can assume that the objects will be aligned to 4-byte boundaries, so we end up with 36 bytes per object. Besides that the voxel grids must also store a reference to the object, which effectively adds another 4 bytes somewhere else in memory, increasing the total to 40 bytes per voxel.

So we end up saving 8 bytes out of 40, reducing the total to 32 bytes. That's a 20% reduction, which is not bad at all.

Why can gaps appear in my line?

Gaps can appear in thin lines when you happen to connect two voxels diagonally, because we decided to always disconnect voxels for those ambiguous cell types. That we're now figuring out edge connections does not change this, but it makes it more obvious that sometimes these voxel should actually have been connected. This is something that we'll deal with in the next tutorial.

Shouldn't we use a boolean?

You could certainly use a boolean. The you have to add two additional boolean variables to Voxel. That might increase the memory size of the object, but due to the 4-byte alignment you could probably store up to three extra boolean variables without actually changing its size.

However, using a negative value to indicate a special case is also perfectly fine, as long as you know what you're doing. In this case negative values are clearly special, as local positions cannot be negative. Typically -1 is used, but we couldn't because a dummy offset could transform that into an invalid positive value.