Rolling

Clamping Velocity Delta

To remove the bias we have to make the velocity adjustment of all dimensions interdependent. So we'll switch to working with an adjustment vector instead of isolated old and new values. While we're at it, let's also swap the components of sideways and vertical movement, so Y is up-down in MovingSphere.Update.

		playerInput.x = Input.GetAxis("Horizontal");
		playerInput.z = Input.GetAxis("Vertical");
		playerInput.y = Swimming ? Input.GetAxis("UpDown") : 0f;

Next, remove the current X and Z values from AdjustVelocity, replacing them with an adjustment vector where we directly calculate the desired velocity adjustment along X and Z.

		Vector3 relativeVelocity = velocity - connectionVelocity;
		//float currentX = Vector3.Dot(relativeVelocity, xAxis);
		//float currentZ = Vector3.Dot(relativeVelocity, zAxis);

		Vector3 adjustment;
		adjustment.x =
			playerInput.x * speed - Vector3.Dot(relativeVelocity, xAxis);
		adjustment.z =
			playerInput.z * speed - Vector3.Dot(relativeVelocity, zAxis);

Also include the Y adjustment at this point, if we're swimming. Otherwise it's zero.

		adjustment.z =
			playerInput.z * speed - Vector3.Dot(relativeVelocity, zAxis);
		adjustment.y = Swimming ?
			playerInput.y * speed - Vector3.Dot(relativeVelocity, upAxis) : 0f;

Then instead of calculating new values for X and Z independently we clamp the adjustment vector by the maximum speed change. This applies acceleration once and removes the bias.

		//float maxSpeedChange = acceleration * Time.deltaTime;

		//float newX =
		//	Mathf.MoveTowards(currentX, playerInput.x * speed, maxSpeedChange);
		//float newZ =
			//Mathf.MoveTowards(currentZ, playerInput.y * speed, maxSpeedChange);

		adjustment =
			Vector3.ClampMagnitude(adjustment, acceleration * Time.deltaTime);

The velocity change is now the X plus Z axes scaled by their respective adjustments.

		velocity += xAxis * adjustment.x + zAxis * adjustment.z;

Plus the adjustment along the Y axis, if needed.

		if (Swimming) {
			//float currentY = Vector3.Dot(relativeVelocity, upAxis);
			//float newY = Mathf.MoveTowards(
			//	currentY, playerInput.z * speed, maxSpeedChange
			//);
			velocity += upAxis * adjustment.y;
		}

This new approach also replaces the sharp sideways zigzag motion with a smooth curve. This is more realistic, as it makes turning at higher velocities more difficult, but it also makes control less precise. You can compensate for this by increasing max acceleration.

Ball Child

To make rolling obvious we need to apply a texture to the sphere. Here is a texture for this purpose. It's a 512×256 texture designed to be wrapped around a sphere, with an arrow or track-like stripe in the middle and red-green coloration for its left and right sides. Apply it to the sphere materials that we have and set the albedo of the normal material to white.

The moving sphere itself doesn't rotate, we'll give it a ball child object instead. Begin by removing the mesh renderer and filter components from the sphere prefab.

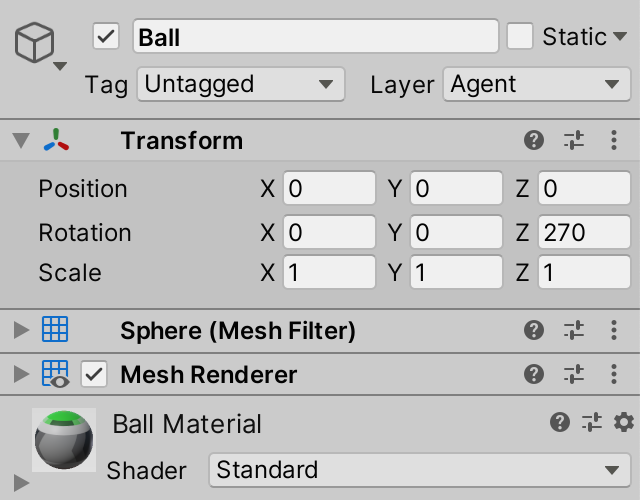
Then add a ball child object to it, which is a default sphere with its collider removed. The default sphere mesh is a cube sphere with default sphere UV coordinates, so the texture is subject to heavy distortion at the poles. For this reason we rotate the ball by 270° around the Z axis, putting the poles on the sides, which matches the uniformly-colored red and green regions of the texture.

Adjusting Ball Materials

From now on we have to change the ball's material instead of the sphere's. Add a configuration option for the ball's Transform component to MovingSphere and get its MeshRenderer in Awake. Then hook up the reference in the prefab.

	[SerializeField]
	Transform playerInputSpace = default, ball = default;

	…
	
	void Awake () {
		body = GetComponent<Rigidbody>();
		body.useGravity = false;
		meshRenderer = ball.GetComponent<MeshRenderer>();
		OnValidate();
	}

At this point we have a textured ball, which makes it obvious that it slides.

Let's put all the code related to updating the ball in a separate UpdateBall method. Move the material-setting code there. Also, switch to using conditional blocks, as we'll make more changes based on the movement mode later.

	void Update () {
		…

		//meshRenderer.material =
			//Climbing ? climbingMaterial :
			//Swimming ? swimmingMaterial : normalMaterial;
		UpdateBall();
	}

	void UpdateBall () {
		Material ballMaterial = normalMaterial;
		if (Climbing) {
			ballMaterial = climbingMaterial;
		}
		else if (Swimming) {
			ballMaterial = swimmingMaterial;
		}
		meshRenderer.material = ballMaterial;
	}

Motion

To make the ball roll we have to rotate it so its surface movement matches its motion. The simplest perfect case is a ball rolling in a straight line. Only a single point of the ball's surface touches the ground at each moment. As the sphere moves forward it rotates, and once it has completed a full rotation of 360° the same point touches the ground again. During that time the point traveled in a circle relative to the ball's origin. Thus the distance traveled equals the circumference of that circle, which is 2π times the radius of the ball.

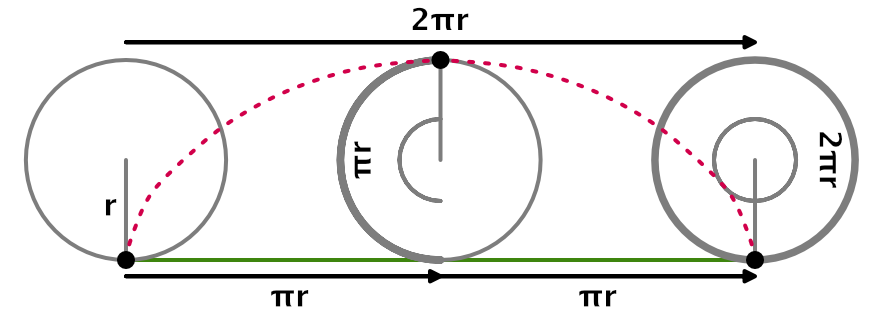
This means that we need to know the radius of the ball, which depends on the sphere's size. Let's add a configuration option for it, which must be positive, set to 0.5 by default, matching the default sphere.

	[SerializeField, Min(0.1f)]
	float ballRadius = 0.5f;

We make the ball roll during the regular per-frame update—in UpdateBall—because it's purely a visual effect. But the sphere moves during the physics steps, so we might end up with linear motion in between if the frame rate is high enough. That's fine as long as the sphere's Rigidbody is set to interpolate. We can then find the appropriate movement vector by dividing the body's velocity by the time delta. The covered distance is the magnitude of that vector. This isn't perfect but it's good enough visually.

	void UpdateBall () {
		…

		Vector3 movement = body.velocity * Time.deltaTime;
		float distance = movement.magnitude;
	}

The corresponding rotation angle is then the distance times 180 divided by π, then divided by the radius. To make the ball roll we create a rotation of that angle via Quaternion.Euler, multiply that with the ball's rotation, and use that as its new rotation. Initially we'll use the world X axis for the rotation axis.

		float distance = movement.magnitude;
		float angle = distance * (180f / Mathf.PI) / ballRadius;
		ball.localRotation =
			Quaternion.Euler(Vector3.right * angle) * ball.localRotation;

Rotation Axis

This approach works, as long as we're moving forward along the world Z axis. To make it work for any direction we have to derive the rotation axis from the movement direction and the contact normal. As the contact normal gets cleared to zero each physics step we'll have to keep track of the last one. Copy the normal to a field just before we clear it.

	Vector3 lastContactNormal;

	…
	
	void ClearState () {
		lastContactNormal = contactNormal;
		…
	}

Now we can find the rotation axis in UpdateBall by taking the cross product of the last contact normal and the movement vector, normalizing the result.

		Vector3 rotationAxis =
			Vector3.Cross(lastContactNormal, movement).normalized;
		ball.localRotation =
			Quaternion.Euler(rotationAxis * angle) * ball.localRotation;

However, this won't work when standing still, so abort if there is very little movement that frame, say less than 0.001.

		float distance = movement.magnitude;
		if (distance < 0.001f) {
			return;
		}

Aligning the Ball

The ball now rotates correctly, but a consequence of this is that its texture can end up with an arbitrary orientation. As its pattern has an implied direction let's make the ball align itself with its forward movement. This requires an additional rotation that gets applied on top of rolling. How quickly it aligns itself can be made configurable, just like the align speed of the orbit camera, so add an option for that.

	[SerializeField, Min(0f)]
	float ballAlignSpeed = 180f;

Copy OrbitCamera.UpdateGravityAlignment to MovingSphere, rename it to AlignBallRotation and adjust it so it works for the ball. Give it two parameters, first the rotation axis and second the ball's rotation. Replace the gravity alignment with the ball's local up axis and gravity with the rotation axis. Finally, apply the adjustment to the ball's rotation and return it.

	Quaternion AlignBallRotation (Vector3 rotationAxis, Quaternion rotation) {
		Vector3 ballAxis = ball.up;
		float dot = Mathf.Clamp(Vector3.Dot(ballAxis, rotationAxis), -1f, 1f);
		float angle = Mathf.Acos(dot) * Mathf.Rad2Deg;
		float maxAngle = ballAlignSpeed * Time.deltaTime;

		Quaternion newAlignment =
			Quaternion.FromToRotation(ballAxis, rotationAxis) * rotation;
		if (angle <= maxAngle) {
			return newAlignment;
		}
		else {
			return Quaternion.SlerpUnclamped(
				rotation, newAlignment, maxAngle / angle
			);
		}
	}

Invoke the method in UpdateBall if the align speed is positive.

		Vector3 rotationAxis =
			Vector3.Cross(lastContactNormal, movement).normalized;
		Quaternion rotation =
			Quaternion.Euler(rotationAxis * angle) * ball.localRotation;
		if (ballAlignSpeed > 0f) {
			rotation = AlignBallRotation(rotationAxis, rotation);
		}
		ball.localRotation = rotation;

This works, but it makes more sense if the alignment is based on traveled distance rather than time. That way the alignment slows down and speeds up along with motion. So pass the distance to AlignBallRotation and use it instead of the time delta. Thus the configured speed is in degrees per traveled unit, rather than per second.

	void UpdateBall () {
		…
		if (ballAlignSpeed > 0f) {
			rotation = AlignBallRotation(rotationAxis, rotation, distance);
		}
		ball.localRotation = rotation;
	}

	Quaternion AlignBallRotation (
		Vector3 rotationAxis, Quaternion rotation, float traveledDistance
	) {
		Vector3 ballAxis = ball.up;
		float dot = Mathf.Clamp(Vector3.Dot(ballAxis, rotationAxis), -1f, 1f);
		float angle = Mathf.Acos(dot) * Mathf.Rad2Deg;
		float maxAngle = ballAlignSpeed * traveledDistance;

		…
	}

Steep Slopes

As we use the last contact normal to derive the rotation axis, when in the air the balls roll as if it were on flat ground. This happens even when the ball slides along a wall.

Although this is correct, it would look more interesting if the sphere would align itself so it rolls along the wall's surface. This would also provide a hint that it's possible to jump off the wall. To make this possible we also have to keep track of the last steep normal.

	Vector3 lastContactNormal, lastSteepNormal;

	…

	void ClearState () {
		lastContactNormal = contactNormal;
		lastSteepNormal = steepNormal;
		…
	}

Now we can end up using different normals to determine our rotation plane in UpdateBall. The default is to use the last contact normal, but if we're not climbing nor swimming, are not on the ground, but are on a steep surface, then use the last steep normal instead.

		Vector3 rotationPlaneNormal = lastContactNormal;
		if (Climbing) {
			ballMaterial = climbingMaterial;
		}
		else if (Swimming) {
			ballMaterial = swimmingMaterial;
		}
		else if (!OnGround) {
			if (OnSteep) {
				rotationPlaneNormal = lastSteepNormal;
			}
		}
		…
		Vector3 rotationAxis =
			Vector3.Cross(rotationPlaneNormal, movement / distance);

Ignoring Upward Motion

Currently we use movement in all three dimensions to determine the ball's rotation and alignment. This means that relative upward and downward motion affects it. Unfortunately this can cause trouble when jumping straight up, especially in complex situations where gravity isn't uniform. Jumping straight up can result in small jittery motion, which leads to erratic ball rotation.

We can reduce this effect by ignoring the relative vertical motion when updating the ball, which is done by projecting the movement on the rotation plane normal and subtracting that from the vector.

		Vector3 movement = body.velocity * Time.deltaTime;
		movement -=
			rotationPlaneNormal * Vector3.Dot(movement, rotationPlaneNormal);

Air and Swim Rotation

If makes sense that the ball rolls when moving along a surface, but when in the air or swimming it technically doesn't need to roll. However, as our sphere is self-propelled it's intuitive that it always rolls. But when not in direct contact with a surface its rotation has no surface to match, so we could make it rotate at a different speed.

Add separate configuration options for the ball's air and swim rotation. At minimum the speeds could be zero. Let's set the air rotation to 0.5 by default, which makes the ball rotate slower while in the air. And let's use 2 for the default swim rotation factor, so the ball appears to work harder while swimming.

	[SerializeField, Min(0f)]
	float
		ballAirRotation = 0.5f,
		ballSwimRotation = 2f;

We adjust the rotation speed by scaling the angle by a rotation factor in UpdateBall. It's 1 by default, but we should use the appropriate configured speed when either swimming or when not in contact with anything.

		float rotationFactor = 1f;
		if (Climbing) {
			ballMaterial = climbingMaterial;
		}
		else if (Swimming) {
			ballMaterial = swimmingMaterial;
			rotationFactor = ballSwimRotation;
		}
		else if (!OnGround) {
			if (OnSteep) {
				rotationPlaneNormal = lastSteepNormal;
			}
			else {
				rotationFactor = ballAirRotation;
			}
		}
		…
		float angle = distance * rotationFactor * (180f / Mathf.PI) / ballRadius;

Rolling on Moving Surfaces

The last step of making our sphere roll correctly is to make it work in combination with moving surfaces. Right now the ball inherits the movement of the connected body, which makes it rotate inappropriately.

To compensate for the surface motion we have to keep track of the last connection velocity.

	Vector3 lastContactNormal, lastSteepNormal, lastConnectionVelocity;

	…

	void ClearState () {
		lastContactNormal = contactNormal;
		lastSteepNormal = steepNormal;
		lastConnectionVelocity = connectionVelocity;
		…
	}

Then we can subtract is from the body's velocity in UpdateBall.

		Vector3 movement =
			(body.velocity - lastConnectionVelocity) * Time.deltaTime;

Rotating Along With Surfaces

Besides moving, the connected body could also rotate. We take this into consideration when determining movement, but the sphere's alignment is not yet affected by it.

In this case we can make the ball rotate along with the platform by creating a rotation from the connected body's angular velocity, scaled by the time delta. We can use the Rigidbody.angularVelocity property for this, which is in radians to we have to multiply it with Mathf.Rad2Deg before we pass it to Quaternion.Euler. Multiply this rotation with the ball's current rotation before rolling it. We only have to do this when we're staying connected to a body, but if so also when the ball is standing still.

		Quaternion rotation = ball.localRotation;
		if (connectedBody && connectedBody == previousConnectedBody) {
			rotation = Quaternion.Euler(
				connectedBody.angularVelocity * (Mathf.Rad2Deg * Time.deltaTime)
			) * rotation;
			if (distance < 0.001f) {
				ball.localRotation = rotation;
				return;
			}
		}
		else if (distance < 0.001f) {
			return;
		}

		float angle = distance * rotationFactor * (180f / Mathf.PI) / ballRadius;
		Vector3 rotationAxis =
			Vector3.Cross(rotationPlaneNormal, movement).normalized;
		//Quaternion rotation =
		rotation = Quaternion.Euler(rotationAxis * angle) * rotation;

As this is a 3D rotation it makes the ball inherit any rotation of the connected body. So if the surface wobbles the ball will wobble along with it.

This concludes the Movement series. The next step from here would be to replace the ball with a more complex body, like a human. That's the subject of a follow-up series that I'll create in the future.