Octasphere

Superior Lat/Lon Sphere

Combine cube sphere and UV sphere algorithms.
Fold rhombuses to create an octahedron.
Derive texture coordinates from vertex position.

This is the eighth tutorial in a series about procedural meshes. This time we create an octahedron sphere as an alternative to the UV sphere.

This tutorial is made with Unity 2020.3.23f1.

An octasphere with a lat/lon texture applied to it.

Octahedron

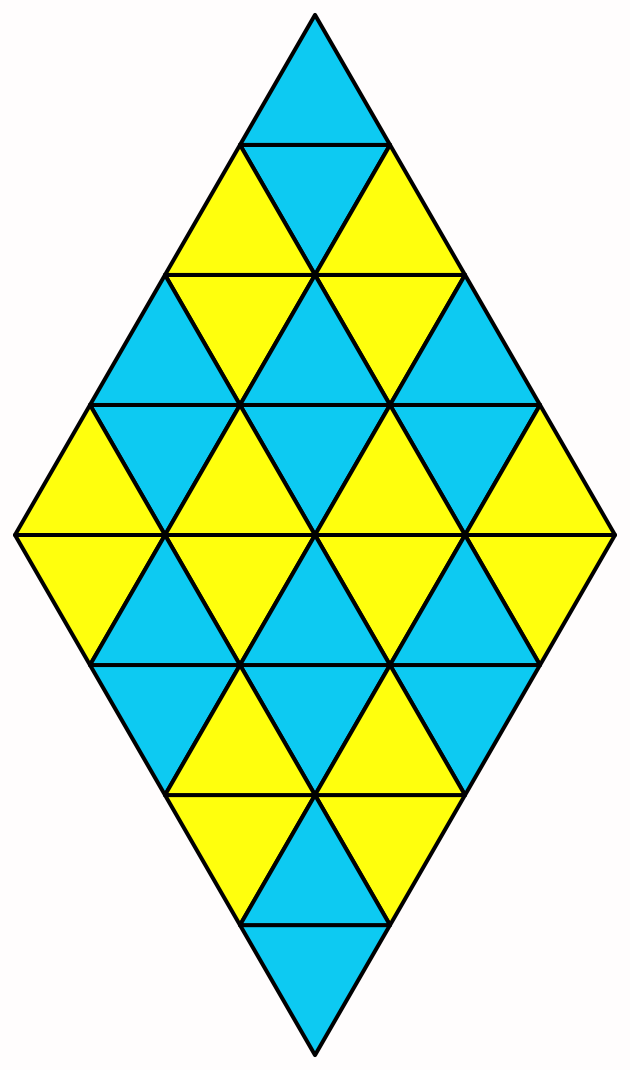
The cube sphere has much better vertex distribution than a UV sphere, but it is not a good candidate when you want to apply a lat/lon texture to a sphere. An alternative is to use what's commonly known as an octasphere, which is a sphere based on an octahedron. We can be sure that this will work because a resolution 1 UV sphere is an octahedron.

Hybrid Approach

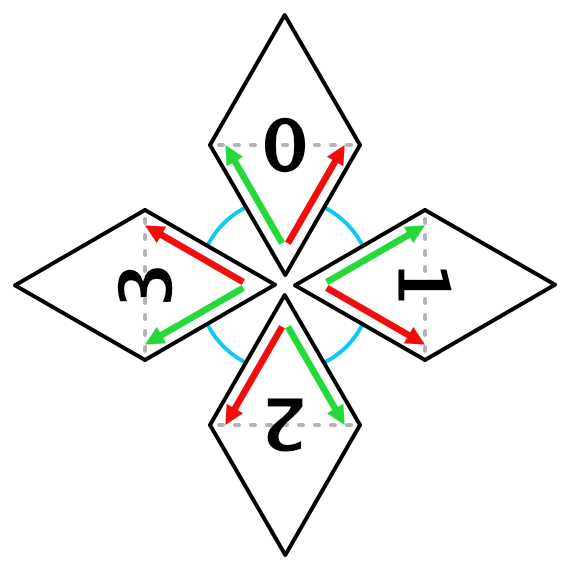
One way to construct an octasphere is to use an approach that is a hybrid of the cube sphere and the UV sphere: create four folded rhombus grids similar to the sides of a cube sphere, positioned and anchored to the poles like the columns of a UV sphere.

We'll use SharedCubeSphere as the basis of the new approach. Duplicate its asset file and rename it to Octasphere.

	public struct Octasphere : IMeshGenerator { … }

Also add an option for it to ProceduralMesh.

	static MeshJobScheduleDelegate[] jobs = {
		…
		MeshJob<SharedCubeSphere, PositionStream>.ScheduleParallel,
		MeshJob<Octasphere, SingleStream>.ScheduleParallel,
		MeshJob<UVSphere, SingleStream>.ScheduleParallel
	};

	public enum MeshType {
		SquareGrid€, SharedSquareGrid€, SharedTriangleGrid€,
		FlatHexagonGrid€, PointyHexagonGrid€, CubeSphere€, SharedCubeSphere€,
		Octasphere€, UVSphere€
	};

Four Sides

Instead of having six square sides an octahedron has eight equilateral triangle sides. We'll generate these in pairs, by creating four folded rhombuses. Let's rename the Side struct, method, and variable to make this clear. Note that I don't show the replacement of all variable references in Execute.

		struct Rhombus {
			public int id;
			…
		}
		
		public void Execute<S> (int i, S streams) where S : struct, IMeshStreams {
			int u = i / 6;
			Rhombus rhombus = GetRhombus(i - 6 * u);
			…
		}
		
		static Rhombus GetRhombus (int id) => id switch { … };

As we go from six down to four sides the vertex count reduces accordingly. So that's `4r^2` instead of `6r^2` vertices for the rhombuses, where `r` is the resolution. However, as we'll support lat/lon maps we also need a seam like the UV sphere has, which requires an additional `2r-1` vertices. Finally, the cube sphere has two polar vertices, but because of the lat/lon map these cannot be shared, so we need eight vertices for the poles, two per rhombus. Thus the final vertex count is `4r^2+2r+7`.

		public int VertexCount => 4 * Resolution * Resolution + 2 * Resolution + 7;

The index count reduces from six to four sides.

		public int IndexCount => 6 * 4 * Resolution * Resolution;

The job length is reduced likewise, but we also add one special case for the seam, like we did for the UV sphere.

		public int JobLength => 4 * Resolution + 1;

Next, update the U coordinate, rhombus identifier, and vertex index at the start of Execute to match the new vertex count and job length. The polar and seam vertices come first, so we have to skip those.

			int u = i / 4;
			Rhombus rhombus = GetRhombus(i - 4 * u);
			int vi = Resolution * (Resolution * rhombus.id + u + 2) + 7;

Finally, remove all the vertex and triangle calculations specific to the cube, while keeping the code that fills the streams. This will produce a degenerate mesh. Because the polar vertices aren't shared we don't need to split the quad that we add outside the loop, so we'll set both its triangles at the end.

		public void Execute<S> (int i, S streams) where S : struct, IMeshStreams {
			int u = i / 4;
			Rhombus rhombus = GetRhombus(i - 4 * u);
			int vi = Resolution * (Resolution * rhombus.id + u + 2) + 7;
			int ti = 2 * Resolution * (Resolution * rhombus.id + u);
			bool firstColumn = u == 0;
			u += 1;

			//float3 pStart = rhombus.uvOrigin + rhombus.uVector * u / Resolution;
			
			var vertex = new Vertex();
			//…
			streams.SetVertex(vi, vertex);
			//…
			vi += 1;
			//ti += 1;

			//…

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				//vertex.position = CubeToSphere(pStart + side.vVector * v / Resolution);
				streams.SetVertex(vi, vertex);
				
				//…
				streams.SetTriangle(ti + 0, 0);
				streams.SetTriangle(ti + 1, 0);
			}

			streams.SetTriangle(ti + 0, 0);
			streams.SetTriangle(ti + 1, 0);
		}
		
		//static float3 CubeToSphere (float3 p) => …;

Poles and Seam

We'll first take care of the vertices for the poles and the seam. We reuse the approach of the UV sphere, introducing a dedicated method for job index zero, this time naming it ExecutePolesAndSeams. To keep the logic for ExecuteRegular the same, subtract one from the job index before passing it to the method.

		public void Execute<S> (int i, S streams) where S : struct, IMeshStreams {
			if (i == 0) {
				ExecutePolesAndSeam(streams);
			}
			else {
				ExecuteRegular(i - 1, streams);
			}
		}

		public void ExecuteRegular<S> (int i, S streams) where S : struct, IMeshStreams {
			int u = i / 4;
			…
		}

		public void ExecutePolesAndSeam<S> (S streams) where S : struct, IMeshStreams {}

The polar vertices for the UV sphere were special, because we have to set their tangent and texture coordinates halfway between their adjacent vertex columns to keep the texture correct. We have to do the same thing here as well, exactly like for a resolution 1 UV sphere. Begin by configuring the tangent and texture X coordinate for the first rhombus, the one going from the back corner to the right corner. Don't set the vertex yet.

		public void ExecutePolesAndSeam<S> (S streams) where S : struct, IMeshStreams {
			var vertex = new Vertex();
			vertex.tangent = float4(sqrt(0.5f), 0f, sqrt(0.5f), -1f);
			vertex.texCoord0.x = 0.125f;
		}

Follow this with a loop over all four south pole vertices, setting the position, normal, and texture Y coordinate. Then set the vertex, rotate the tangent 90° and increment the texture X coordinate by ¼ for the next iteration. We'll assign them to the first four vertices.

			var vertex = new Vertex();
			vertex.tangent = float4(sqrt(0.5f), 0f, sqrt(0.5f), -1f);
			vertex.texCoord0.x = 0.125f;

			for (int i = 0; i < 4; i++) {
				vertex.position = vertex.normal = down();
				vertex.texCoord0.y = 0f;
				streams.SetVertex(i, vertex);
				vertex.tangent.xz = float2(-vertex.tangent.z, vertex.tangent.x);
				vertex.texCoord0.x += 0.25f;
			}

The north pole vertices are the same, but at the top of the sphere. We can set them in the same loop, using the next four vertices.

			for (int i = 0; i < 4; i++) {
				vertex.position = vertex.normal = down();
				vertex.texCoord0.y = 0f;
				streams.SetVertex(i, vertex);
				vertex.position = vertex.normal = up();
				vertex.texCoord0.y = 1f;
				streams.SetVertex(i + 4, vertex);
				vertex.tangent.xz = float2(-vertex.tangent.z, vertex.tangent.x);
				vertex.texCoord0.x += 0.25f;
			}

After that come the vertices of the seam. Begin by creating a line from the south pole to the back corner of the octahedron, via linear interpolation.

			for (int i = 0; i < 4; i++) { … }

			vertex.tangent.xz = float2(1f, 0f);
			vertex.texCoord0.x = 0f;

			for (int v = 1; v < 2 * Resolution; v++) {
				vertex.position = lerp(down(), back(), (float)v / (2 * Resolution));
				vertex.normal = normalize(vertex.position);
				streams.SetVertex(v + 7, vertex);
			}

This puts all seam vertices on the bottom half of the octahedron. To make them go all the way to the top we can double the interpolator, so it extrapolates past the end point.

				vertex.position = lerp(down(), back(), (float)v / Resolution);

This gives us a seams as if our octahedron were pulled open at the top. To close it we have to switch to a different interpolation for the second half of the loop, going from the back corner to the north pole, and also resetting the interpolator.

				if (v < Resolution) {
					vertex.position = lerp(down(), back(), (float)v / Resolution);
				}
				else {
					vertex.position =
						lerp(back(), up(), (float)(v - Resolution) / Resolution);
				}

Rhombuses

Moving on to the four rhombuses, we need to know their orientation. We can define this by adding positions for their middle left and right corners to Rhombus. We don't need anything else besides the identifier, so remove all those fields.

		struct Rhombus {
			public int id;
			public float3 leftCorner, rightCorner;

			//public float3 uvOrigin, uVector, vVector;
			//public int seamStep;

			//public bool TouchesMinimumPole => (id & 1) == 0;
		}

Going counterclockwise around the sphere, the four corner pairs are back-right, right-forward, forward-left, and left-back. Adjust GetRhombus accordingly.

		static Rhombus GetRhombus (int id) => id switch {
			0 => new Rhombus {
				id = id,
				leftCorner = back(),
				rightCorner = right()
			},
			1 => new Rhombus {
				id = id,
				leftCorner = right(),
				rightCorner = forward()
			},
			2 => new Rhombus {
				id = id,
				leftCorner = forward(),
				rightCorner = left()
			},
			//3 => new Rhombus {  },
			//4 => new Rhombus {  },
			_ => new Rhombus {
				id = id,
				leftCorner = left(),
				rightCorner = back()
			}
		};

Now we can set the position of the first vertex inside ExecuteRegular, which defines the bottom vertex of each column. We set this position by interpolating from the south pole to the right corner based on U. We'll focus on the positions only for now, leaving the other vertex attributes for later.

			var vertex = new Vertex();
			vertex.position = lerp(down(), rhombus.rightCorner, (float)u / Resolution);
			streams.SetVertex(vi, vertex);

To create a complete rhombus we also need to interpolate based on V inside the loop. Let's first build a flat rhombus. We can do this by also determining the end of the column before the loop begins. In the case of a flat rhombus the column end has to interpolate in the same direction as the column start, so let's replace the usage of lerp with the application of a column direction vector.

			float3 columnDir = rhombus.rightCorner - down();

			var vertex = new Vertex();
			vertex.position = down() + columnDir * u / Resolution;

Now we can determine both start and end by adding to the appropriate positions and store them in variables. To find the column end we have to begin at the left corner instead of at the south pole.

			float3 columnDir = rhombus.rightCorner - down();
			float3 columnStart = down() + columnDir * u / Resolution;
			float3 columnEnd = rhombus.leftCorner + columnDir * u / Resolution;

			var vertex = new Vertex();
			vertex.position = columnStart;

This makes it possible to interpolate through the column inside the loop.

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				vertex.position = lerp(columnStart, columnEnd, (float)v / Resolution);
				streams.SetVertex(vi, vertex);
				streams.SetTriangle(ti + 0, 0);
				streams.SetTriangle(ti + 1, 0);
			}

Closing the Octahedron

At this point we have an open octahedron. We can close it like we closed the seam. First, let's make explicit that what we currently have works for the bottom half of the rhombus, by renaming our variables.

			float3 columnBottomDir = rhombus.rightCorner - down();
			float3 columnBottomStart = down() + columnBottomDir * u / Resolution;
			float3 columnBottomEnd =
				rhombus.leftCorner + columnBottomDir * u / Resolution;

			var vertex = new Vertex();
			vertex.position = columnBottomStart;
			streams.SetVertex(vi, vertex);
			vi += 1;

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				vertex.position =
					lerp(columnBottomStart, columnBottomEnd, (float)v / Resolution);
				…
			}

Then introduce alternatives for the top half of the rhombus, based on going from the left corner to the north pole instead of from the south pole to the right corner. In this case the starting points are the right corner and the left corner.

			float3 columnBottomDir = rhombus.rightCorner - down();
			float3 columnBottomStart = down() + columnBottomDir * u / Resolution;
			float3 columnBottomEnd =
				rhombus.leftCorner + columnBottomDir * u / Resolution;

			float3 columnTopDir = up() - rhombus.leftCorner;
			float3 columnTopStart = rhombus.rightCorner + columnTopDir * u / Resolution;
			float3 columnTopEnd = rhombus.leftCorner + columnTopDir * u / Resolution;

Adjust the loop so it generated the top portion.

				vertex.position =
					lerp(columnTopStart, columnTopEnd, (float)v / Resolution);

This should give us a closed top and open bottom, but it went wrong. That happened because our top start should begin outside of the octahedron, because we're going in the opposite direction compared to the bottom scenario. We can achieve that via extrapolation, by subtracting 1 from the factor by which we multiply the direction vector for the top.

			float3 columnTopStart =
				rhombus.rightCorner + columnTopDir * ((float)u / Resolution - 1f);

With both sides correct all that's left is to pick the correct one for each iteration. In this case the halfway point is reached when V equals the resolution minus U.

				if (v <= Resolution - u) {
					vertex.position =
						lerp(columnBottomStart, columnBottomEnd, (float)v / Resolution);
				}
				else {
					vertex.position =
						lerp(columnTopStart, columnTopEnd, (float)v / Resolution);
				}

Triangles

With all the vertices of the octahedron in place we can generate its triangles. The complexity of this work lies somewhere in between the cube sphere and the UV sphere.

Rhombus Quads

Although an octasphere is made with triangles and not squares, we can also say that it's made with folded rhombuses, as long as we orient their triangles correctly.

So we can create quads again and this time we'll use an int4 variable to hold all four indices at once. We'll use the following vertex order: right, bottom, left, top. The first triangle of each quad uses the XYZ components and the second triangle uses the XZW components. Adjust ExecuteRegular to use this approach, initially generating degenerate triangles with all indices set to zero.

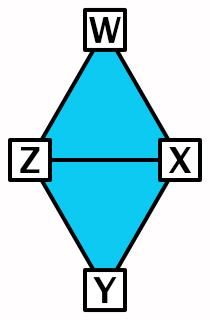
			int4 quad = 0;
			
			u += 1;
			
			…

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				…
				streams.SetTriangle(ti + 0, quad.xyz);
				streams.SetTriangle(ti + 1, quad.xzw);
			}
			
			streams.SetTriangle(ti + 0, quad.xyz);
			streams.SetTriangle(ti + 1, quad.xzw);

Seam Column

We begin with the first quad of the first column of the first rhombus, the one touching the south pole. Its first vertex X is the current one. Its second vertex Y is the first south pole vertex, which is the first of the mesh. Its third vertex Z is the first seam vertex after the poles, so index 8. The final vertex W is the one after X. Set these if we're in the first column of the first rhombus, keeping all other quads degenerate for now.

			int4 quad = 0;
			if (firstColumn && rhombus.id == 0) {
				quad.x = vi;
				quad.y = 0;
				quad.z = 8;
				quad.w = vi + 1;
			}

This column runs along the bottom part of the seam, so we can simply increment all the quad's indices inside the loop, except for Y, which has to become equal to Z first.

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				…
				streams.SetTriangle(ti + 0, quad.xyz);
				streams.SetTriangle(ti + 1, quad.xzw);

				quad.y = quad.z;
				quad += int4(1, 0, 1, 1);
			}

The only thing that's missing is the top part of the last rhombus, because it lies inside the top half of the rhombus. We can set its W correctly by making it equal to Z plus 1 after the loop.

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) { … }

			if (firstColumn && rhombus.id == 0) {
				quad.w = quad.z + 1;
			}

			streams.SetTriangle(ti + 0, quad.xyz);
			streams.SetTriangle(ti + 1, quad.xzw);

First Rhombus

Next, always initialize the quad if we're working on the first rhombus. If we're not in the first column then Y should be one column below X and Z is simply one step after that.

			int4 quad = 0;
			if (rhombus.id == 0) {
				quad.x = vi;
				quad.y = firstColumn ? 0 : vi - Resolution;
				quad.z = firstColumn ? 8 : vi - Resolution + 1;
				quad.w = vi + 1;
			}

This works for everything except the last row, which touches the top half of the seam. To fix this always adjust W for the first rhombus and set Z to the correct seam vertex, which is the resolution plus U plus 6.

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) { … }

			if (rhombus.id == 0) {
				quad.z = Resolution + u + 6;
				quad.w = quad.z + 1;
			}

And to fix the top triangle set W to 4 for the last column, which is the first north pole vertex.

			if (rhombus.id == 0) {
				quad.z = Resolution + u + 6;
				quad.w = u < Resolution ? quad.z + 1 : 4;
			}

All First Columns

Moving on to the other rhombuses, we again begin with their first columns. If we're not working on the first rhombus but are in the first column, then initialize the first quad. In this case X and W are the same as for the first rhombus, while Y is equal to the rhombus identifier. Z wraps to the previous rhombus and thus requires an offset of `-r^2+ru`.

			int4 quad = 0;
			if (rhombus.id == 0) {
				quad.x = vi;
				quad.y = firstColumn ? 0 : vi - Resolution;
				quad.z = firstColumn ? 8 : vi - Resolution + 1;
				quad.w = vi + 1;
			}
			else if (firstColumn) {
				quad.x = vi;
				quad.y = rhombus.id;
				quad.z = vi - Resolution * (Resolution + u);
				quad.w = vi + 1;
			}

Also, when incrementing, if we're working on the first column that isn't of the first rhombus we have to add the resolution instead of 1 to Z, because we're moving along the edge of the previous rhombus.

				quad.y = quad.z;
				quad += int4(1, 0, firstColumn && rhombus.id != 0 ? Resolution : 1, 1);

After the loop, we now also have to also add the rhombus offset to Z, while W is again equal to Z plus 1. Again, we only focus on the first columns of the other rhombuses for now.

			if (rhombus.id == 0) {
				quad.z = Resolution + u + 6;
				quad.w = u < Resolution ? quad.z + 1 : 4;
			}
			else if (firstColumn) {
				quad.z = Resolution + u + 6 + Resolution * Resolution * rhombus.id;
				quad.w = quad.z + 1;
			}
			else {
				quad = 0;
			}

First columns of the 2^nd and 3^rd rhombuses.

Entire Octahedron

To fill all these rhombuses, again apply the initialization for them to all columns. The logic for all other columns is the same as for the first rhombus.

			int4 quad = 0;
			if (rhombus.id == 0) {
				quad.x = vi;
				quad.y = firstColumn ? 0 : vi - Resolution;
				quad.z = firstColumn ? 8 : vi - Resolution + 1;
				quad.w = vi + 1;
			}
			else { //if (firstColumn) {
				quad.x = vi;
				quad.y = firstColumn ? rhombus.id : vi - Resolution;
				quad.z = firstColumn ?
					vi - Resolution * (Resolution + u) : vi - Resolution + 1;
				quad.w = vi + 1;
			}

Likewise for the final quad, we just need to add the rhombus identifier to get the correct north pole vertex.

			if (rhombus.id == 0) {
				quad.z = Resolution + u + 6;
				quad.w = u < Resolution ? quad.z + 1 : 4;
			}
			else { //if (firstColumn) {
				quad.z = Resolution + u + 6 + Resolution * Resolution * rhombus.id;
				quad.w = u < Resolution ? quad.z + 1 : rhombus.id + 4;
			}
			//else {
			//	quad = 0;
			//}

Now that we have a complete octahedron let's consolidate the quad initialization code.

			int4 quad = int4(
				vi,
				firstColumn ? rhombus.id : vi - Resolution,
				firstColumn ?
					rhombus.id == 0 ? 8 : vi - Resolution * (Resolution + u) :
					vi - Resolution + 1,
				vi + 1
			);
			//if (rhombus.id == 0) { … }
			//else { … }

And also the adjustment for the final quad.

			quad.z = Resolution * Resolution * rhombus.id + Resolution + u + 6;
			quad.w = u < Resolution ? quad.z + 1 : rhombus.id + 4;
			//if (rhombus.id == 0) { … }
			//else { … }

Sphere

With the octahedron complete what's left is to turn it into a sphere and make sure that all its vertex data is set correctly.

Positions and Normals

The correct positions and normal vectors are both found by normalizing the octahedron position. This needs to be done inside the loop in ExecutePolesAndSeam.

				vertex.normal = vertex.position = normalize(vertex.position);

And for the first vertex in ExecuteRegular.

			var vertex = new Vertex();
			vertex.normal = vertex.position = normalize(columnBottomStart);

And also inside its column loop.

				if (v <= Resolution - u) { … }
				else { … }
				vertex.normal = vertex.position = normalize(vertex.position);
				streams.SetVertex(vi, vertex);

Tangents

The seam already has tangent vectors. All XZ components of all other tangent vectors can be found by rotating the XZ position of the sphere vertex 90° counterclockwise and normalizing it. Introduce a convenient method for that.

		static float2 GetTangentXZ (float3 p) => normalize(float2(-p.z, p.x));

Use it inside ExecuteRegular, also initializing the tangent W component to −1.

			var vertex = new Vertex();
			vertex.position = normalize(columnBottomStart);
			vertex.tangent.xz = GetTangentXZ(vertex.position);
			vertex.tangent.w = -1f;
			streams.SetVertex(vi, vertex);
			vi += 1;

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				…
				vertex.position = normalize(vertex.position);
				vertex.tangent.xz = GetTangentXZ(vertex.position);
				streams.SetVertex(vi, vertex);
				…
			}

Texture Coordinates

Generating the correct texture coordinates is not as straightforward, as we have to determine the correct mapping for effectively arbitrary points on the unit sphere. When generating the UV sphere we converted from UV coordinates to unit sphere positions. Now we have to do the opposite, which can be done by applying inverse trigonometric functions. Also introduce a convenient method for this.

		static float2 GetTexCoord (float3 p) => float2(
			0f,
			0f,
		);

Use this method to set the texture coordinates in ExecuteRegular.

			vertex.texCoord0 = GetTexCoord(vertex.position);
			streams.SetVertex(vi, vertex);
			vi += 1;

			for (int v = 1; v < Resolution; v++, vi++, ti += 2) {
				…
				vertex.texCoord0 = GetTexCoord(vertex.position);
				streams.SetVertex(vi, vertex);
				…
			}

And also for the seam in ExecutePolesAndSeam, but in this case only set the V coordinate, as the seam's U coordinates are all zero.

				vertex.normal = vertex.position = normalize(vertex.position);
				vertex.texCoord0.y = vertex.texCoord0 = GetTexCoord(vertex.position).y;
				streams.SetVertex(v + 7, vertex);

The V coordinate can be found by calculating the arc sine of the Y coordinate. This gives us an angle in radians with a range of π centered on zero, which we have to convert to the 0–1 range to get the texture coordinate.

		static float2 GetTexCoord (float3 p) => float2(
			0f,
			asin(p.y) / PI + 0.5f
		);

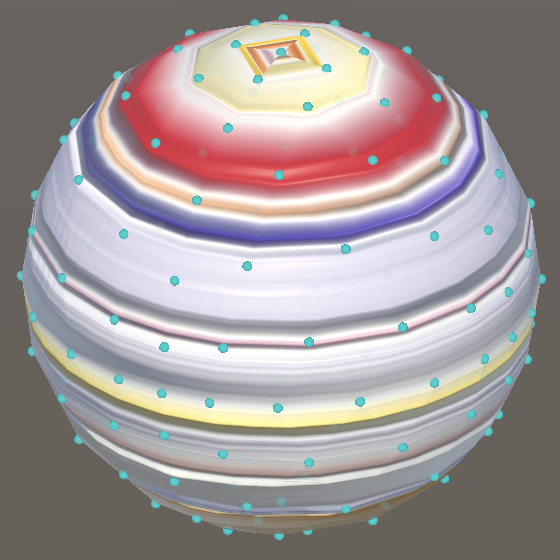
V texture coordinates; *Lat Lon Map* material.

To find the U coordinate we need to apply the arc tangent. We'll use the atan2 method for this, passing it X and Z as arguments. This gives us the arc tangent in radians of X divided by Z, with the result in the correct quadrant. The resulting angle has a range of 2π centered on zero, which we have to convert to the 0–1 range.

		static float2 GetTexCoord (float3 p) => float2(
			atan2(p.x, p.z) / (2f * PI) + 0.5f,
			asin(p.y) / PI + 0.5f
		);

U texture coordinates reversed; *Flat* material.

The result goes in the wrong direction, which is fixed by negating the result of the arc tangent. We can do this by flippin the sign of the constant denominator.

		static float2 GetTexCoord (float3 p) => float2(
			atan2(p.x, p.z) / (-2f * PI) + 0.5f,
			asin(p.y) / PI + 0.5f
		);

Correct direction but incorrect wrapping.

This works except for the right side of the fourth quadrant. The U coordinate wraps back to zero while it should go to 1. We can fix this by checking whether the U coordinate that we calculated is very close to zero—but not too close due to precision limitations—like less than 0.000001. If so, set it to 1. This works because the seam's U coordinates are always zero.

		static float2 GetTexCoord (float3 p) {
			var texCoord = float2(
				atan2(p.x, p.z) / (-2f * PI) + 0.5f,
				asin(p.y) / PI + 0.5f
			);
			if (texCoord.x < 1e-6f) {
				texCoord.x = 1f;
			}
			return texCoord;
		}

The next tutorial is Geodesic Octasphere.

license repository PDF