Value Noise
Lattice Noise
- Create an abstract visualization class.
- Introduce a generic job for noise.
- Generate 1D, 2D, and 3D value noise.
This is the third tutorial in a series about pseudorandom noise. It covers the transition from pure hashing to the simplest form of lattice noise.
This tutorial is made with Unity 2020.3.6f1.
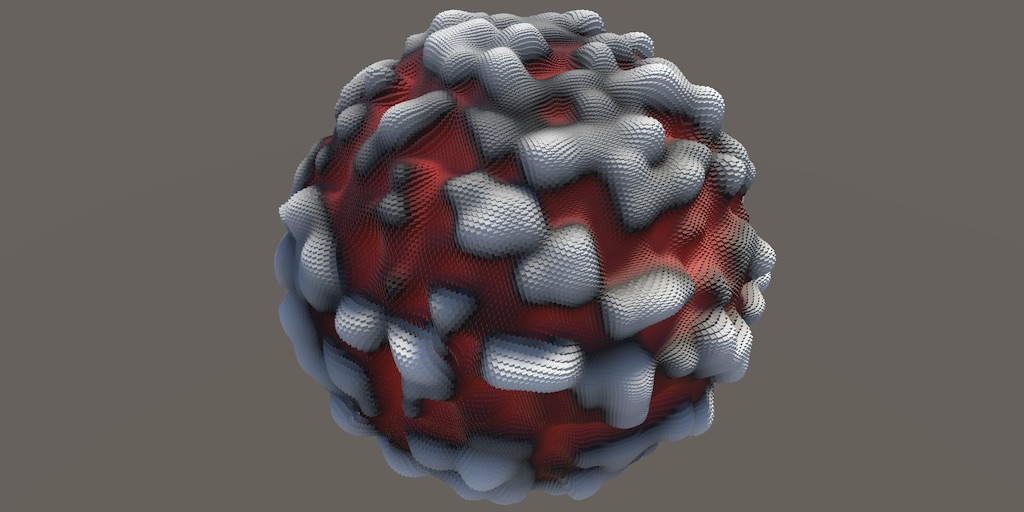
Reusable Visualization
Our hash visualization shows how a hash function partitions space in discrete blocks of values, based on integer coordinates. The idea is that a noise function uses these hash values to produce a pattern that isn't as blocky. We'll specifically implement value noise in this tutorial, which smoothes out the blocky hash pattern. The output of the noise function thus produces a continuous pattern, yielding floating-point values instead of discrete bit patterns. This requires a similar yet different visualization for noise than we currently have.
We could duplicate the code from HashVisualization and reuse that for a NoiseVisualization class, but that would introduce a lot of duplicate code. We'll use inheritance to avoid this redundancy by introducing an abstract Visualization class that will serve as the basis for both hash and noise visualizations.
Abstract Visualization Class
Duplicate the HashVisualization C# asset and rename it to Visualization, then remove the job and all fields that are directly related to hashes, the hash seed, and the hash domain.
//using Unity.Burst;using Unity.Collections; using Unity.Jobs; using Unity.Mathematics; using UnityEngine; using static Unity.Mathematics.math; public class Visualization : MonoBehaviour {//[BurstCompile(FloatPrecision.Standard, FloatMode.Fast, CompileSynchronously = true)]//struct HashJob : IJobFor { … }… static int//hashesId = Shader.PropertyToID("_Hashes"),positionsId = Shader.PropertyToID("_Positions"), normalsId = Shader.PropertyToID("_Normals"), configId = Shader.PropertyToID("_Config"); …//[SerializeField]//int seed;//[SerializeField]//SpaceTRS domain = new SpaceTRS {//scale = 8f//};//NativeArray<uint4> hashes;NativeArray<float3x4> positions, normals;//ComputeBuffer hashesBuffer, positionsBuffer, normalsBuffer;ComputeBuffer positionsBuffer, normalsBuffer; … }
Clean up the OnEnable and OnDisable methods to match.
void OnEnable () {
isDirty = true;
int length = resolution * resolution;
length = length / 4 + (length & 1);
//hashes = new NativeArray<uint4>(length, Allocator.Persistent);
positions = new NativeArray<float3x4>(length, Allocator.Persistent);
normals = new NativeArray<float3x4>(length, Allocator.Persistent);
//hashesBuffer = new ComputeBuffer(length * 4, 4);
positionsBuffer = new ComputeBuffer(length * 4, 3 * 4);
normalsBuffer = new ComputeBuffer(length * 4, 3 * 4);
propertyBlock ??= new MaterialPropertyBlock();
//propertyBlock.SetBuffer(hashesId, hashesBuffer);
…
}
void OnDisable () {
//hashes.Dispose();
positions.Dispose();
normals.Dispose();
//hashesBuffer.Release();
positionsBuffer.Release();
normalsBuffer.Release();
//hashesBuffer = null;
positionsBuffer = null;
normalsBuffer = null;
}
And change OnValidate so it checks the positions buffer instead of the hashes buffer.
void OnValidate () {
if (positionsBuffer != null && enabled) {
OnDisable();
OnEnable();
}
}
Then remove the scheduling of the hash job and setting of the hash buffer from Update.
void Update () {
if (isDirty || transform.hasChanged) {
…
//new HashJob {
// …
//}.ScheduleParallel(hashes.Length, resolution, handle).Complete();
//hashesBuffer.SetData(hashes.Reinterpret<uint>(4 * 4));
…
}
…
}
What we have left is a class that does everything needed for visualization except calculating and storing the data to be visualized. So on its own it is useless and there is no point to attach a component of this type to a game object. To indicate this we mark the class as abstract.
public abstract class Visualization : MonoBehaviour { … }
This makes it impossible to create a direct instance of the Visualization type.
Abstract Methods
Whatever we use Visualization for, it must support being enabled and disabled. It already has OnEnable and OnDisable methods, but those do not create or remove the native arrays, buffers, or whatever else is needed for the data to be visualized. Let's assume that such work is done in dedicated EnableVisualization and DisableVisualization methods and add them to Visualization. As we do not know what code goes in these methods we declare them as abstract signatures only, similar to the contract of an interface. We can do this because the class itself is abstract as well so we can omit parts of its implementation.
abstract void EnableVisualization (); abstract void DisableVisualization ();
When enabling a visualization both the data length and a material property block are needed, so add those as parameter to EnableVisualization.
abstract void EnableVisualization ( int dataLength, MaterialPropertyBlock propertyBlock );
Invoke EnableVisualization once we have a property block in OnEnable. Invoke DisableVisualization at the end of OnDisable.
void OnEnable () {
…
propertyBlock ??= new MaterialPropertyBlock();
EnableVisualization(length, propertyBlock);
…
}
void OnDisable () {
…
DisableVisualization();
}
We also have to perform some yet-unknown work when updating the visualization. Add an abstract UpdateVisualization method for this, with a native array for positions, a resolution, and a job handle as parameters.
abstract void UpdateVisualization ( NativeArray<float3x4> positions, int resolution, JobHandle handle );
Invoke this method in Update, passing it the handle of the shape job.
//JobHandle handle = shapeJobs[(int)shape](//positions, normals, resolution, transform.localToWorldMatrix, default//);UpdateVisualization( positions, resolution, shapeJobs[(int)shape]( positions, normals, resolution, transform.localToWorldMatrix, default ) );
The idea is that our concrete visualizations extend Visualization and provide implementations of the three abstract methods. These classes must be able to access those methods, but that is currently not possible because they are private to Visualization. We could make them public, but that is not needed because they're only used by the class itself. We'll make them protected instead, which means that only the class itself and all classes that extend it can access the methods.
protected abstract void EnableVisualization ( int dataLength, MaterialPropertyBlock propertyBlock ); protected abstract void DisableVisualization (); protected abstract void UpdateVisualization ( NativeArray<float3x4> positions, int resolution, JobHandle handle );
Extending an Abstract Class
We're now going to adjust HashVisualization so it extends Visualization instead of MonoBehaviour directly, thus inheriting all the general-purpose visualization functionality.
public class HashVisualization : Visualization { … }
Remove the nested Shape type and all fields that HashVisualization now inherits from Visualization, as they're now duplicates.
//public enum Shape { Plane, Sphere, Torus }//static Shapes.ScheduleDelegate[] shapeJobs = { … };static int hashesId = Shader.PropertyToID("_Hashes");//positionsId = Shader.PropertyToID("_Positions"),//normalsId = Shader.PropertyToID("_Normals"),//configId = Shader.PropertyToID("_Config");//…[SerializeField] int seed; [SerializeField] SpaceTRS domain = new SpaceTRS { scale = 8f }; NativeArray<uint4> hashes;//NativeArray<float3x4> positions, normals;//ComputeBuffer hashesBuffer, positionsBuffer, normalsBuffer;ComputeBuffer hashesBuffer;//MaterialPropertyBlock propertyBlock;//bool isDirty;//Bounds bounds;
Change OnEnable so it becomes EnableVisualization, only containing the code that deals with the hash data.
void EnableVisualization (int dataLength, MaterialPropertyBlock propertyBlock) {
//…
hashes = new NativeArray<uint4>(dataLength, Allocator.Persistent);
//positions = new NativeArray<float3x4>(length, Allocator.Persistent);
//normals = new NativeArray<float3x4>(length, Allocator.Persistent);
hashesBuffer = new ComputeBuffer(dataLength * 4,4);
//positionsBuffer = new ComputeBuffer(length * 4, 3 * 4);
//normalsBuffer = new ComputeBuffer(length * 4, 3 * 4);
//propertyBlock ??= new MaterialPropertyBlock();
propertyBlock.SetBuffer(hashesId, hashesBuffer);
//…
}
We have to indicate that this method overrides its abstract version, which is done by writing override in front of it. We also have to give it the same protected access level.
protected override void EnableVisualization (
int dataLength, MaterialPropertyBlock propertyBlock
) { … }
Turn OnDisable into DisableVisualization, using the same approach.
protected override void DisableVisualization () {
hashes.Dispose();
//positions.Dispose();
//normals.Dispose();
hashesBuffer.Release();
//positionsBuffer.Release();
//normalsBuffer.Release();
hashesBuffer = null;
//positionsBuffer = null;
//normalsBuffer = null;
}
Remove the OnValidate method, because it's already defined in the base class that we extend.
//void OnValidate () { … }
And finally change Update so it becomes UpdateVisualization, only scheduling and completing the hash job, followed by setting the hashes buffer.
protected override void UpdateVisualization (
NativeArray<float3x4> positions, int resolution, JobHandle handle
) {
//…
new HashJob {
positions = positions,
hashes = hashes,
hash = SmallXXHash.Seed(seed),
domainTRS = domain.Matrix
}.ScheduleParallel(hashes.Length, resolution, handle).Complete();
hashesBuffer.SetData(hashes.Reinterpret<uint>(4 * 4));
//…
}
At this point our hash visualization still works as before, but with all general-purpose visualization code isolated in the separate Visualization class.
Visualizing Noise
We're going to create a new NoiseVisualization component type that also extends Visualization. Do this by duplicating HashVisualization, removing its hash job, and replacing all references to hashes with references to noise. As the noise will consist of floating-point values changes the element type of the native array to float4. Initially have UpdateVisualization only complete the provided handle and sets the noise buffer. This will produce a noise that's zero everywhere.
//using Unity.Burst;using Unity.Collections; using Unity.Jobs; using Unity.Mathematics; using UnityEngine;//using static Unity.Mathematics.math;public class NoiseVisualization : Visualization {//[BurstCompile(FloatPrecision.Standard, FloatMode.Fast, CompileSynchronously = true)]//struct HashJob : IJobFor { … }static int noiseId = Shader.PropertyToID("_Noise"); [SerializeField] int seed; [SerializeField] SpaceTRS domain = new SpaceTRS { scale = 8f }; NativeArray<float4> noise; ComputeBuffer noiseBuffer; protected override void EnableVisualization ( int dataLength, MaterialPropertyBlock propertyBlock ) { noise = new NativeArray<float4>(dataLength, Allocator.Persistent); noiseBuffer = new ComputeBuffer(dataLength * 4, 4); propertyBlock.SetBuffer(noiseId, noiseBuffer); } protected override void DisableVisualization () { noise.Dispose(); noiseBuffer.Release(); noiseBuffer = null; } protected override void UpdateVisualization ( NativeArray<float3x4> positions, int resolution, JobHandle handle ) {//new HashJob {//…//}.ScheduleParallel(hashes.Length, resolution, handle).Complete();handle.Complete(); noiseBuffer.SetData(noise.Reinterpret<float>(4 * 4)); } }
The noise visualization needs a slightly different shader. Duplicate HashGPU and rename it to NoiseGPU. Replace the hashes buffer with a noise buffer and directly use the noise value to offset the position in ConfigureProcedural. This works because our noise values will lie in the −1–1 range.
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
StructuredBuffer<float> _Noise;
StructuredBuffer<float3> _Positions, _Normals;
#endif
float4 _Config;
void ConfigureProcedural () {
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
…
unity_ObjectToWorld._m03_m13_m23 +=
_Config.z * _Noise[unity_InstanceID] * _Normals[unity_InstanceID];
unity_ObjectToWorld._m00_m11_m22 = _Config.y;
#endif
}
Then replace GetHashColor with a GetNoiseColor function that directly returns the noise value if it is positive, producing a grayscale value. If the noise is negative then let's make it a shade of red instead, so it's easy so see the difference between positive and negative noise.
float3 GetNoiseColor () {
#if defined(UNITY_PROCEDURAL_INSTANCING_ENABLED)
float noise = _Noise[unity_InstanceID];
return noise < 0.0 ? float3(-noise, 0.0, 0.0) : noise;
#else
return 1.0;
#endif
}
void ShaderGraphFunction_float (float3 In, out float3 Out, out float3 Color) {
Out = In;
Color = GetNoiseColor();
}
void ShaderGraphFunction_half (half3 In, out half3 Out, out half3 Color) {
Out = In;
Color = GetNoiseColor();
}
Create a shader graph or surface shader for noise, by duplicating the hash version and changing which HLSL file it uses. If you use a surface shader then you also have to change which color function is invoked. Then create a material with it, followed by a game object with the NoiseVisualization component that uses it.
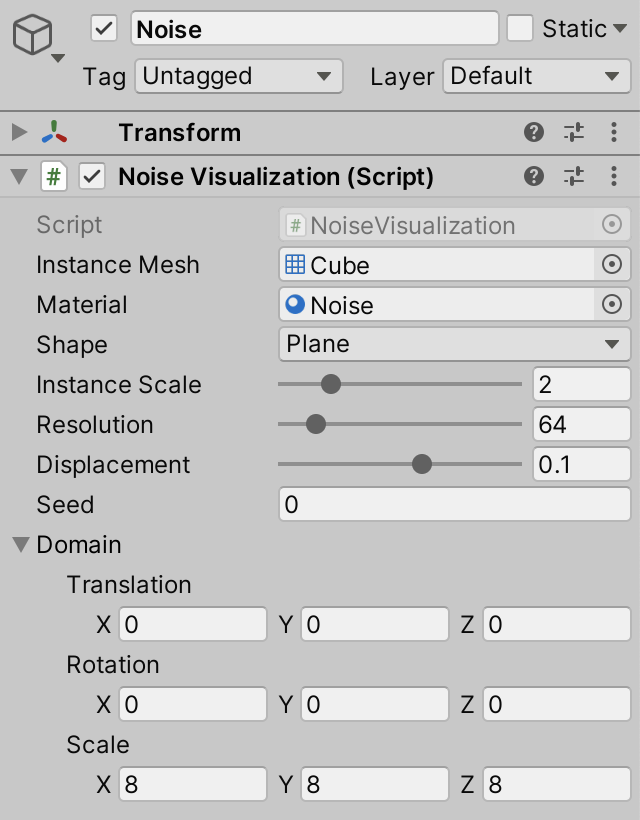
I put the hash and noise visualizations in separate scenes, but you could also have both in the same scene, with only one of them enabled.
Extension Methods
Once we create a job for calculating noise we will have three places where we need to perform a vectorized matrix-vector transformation. Rather than introduce yet another instance of TransformPositions or TransformVectors let's put this code in a single place that we can use everywhere. The simplest way to do this is by creating a static MathExtensions class—in its own C# file—that contains a public static copy of the TransformVectors method from Shapes.Job.
using Unity.Mathematics;
using static Unity.Mathematics.math;
public static class MathExtensions {
public static float4x3 TransformVectors (
float3x4 trs, float4x3 p, float w = 1f
) => float4x3€(
trs.c0.x * p.c0 + trs.c1.x * p.c1 + trs.c2.x * p.c2 + trs.c3.x * w,
trs.c0.y * p.c0 + trs.c1.y * p.c1 + trs.c2.y * p.c2 + trs.c3.y * w,
trs.c0.z * p.c0 + trs.c1.z * p.c1 + trs.c2.z * p.c2 + trs.c3.z * w
);
}
Now we can invoke it everywhere via MathExtensions.TransformVectors(trs, v). This can be reduced to just TransformVectors(trs, v) with the help of using static MathExtensions. However, another way to do this is by turning it into an extension method.
An extension method is a static method that pretends to be an instance method of a type. It is created by adding the this modifier to the first parameter of the method.
public static float4x3 TransformVectors ( this float3x4 trs, float4x3 p, float w = 1f ) => float4x3(…);
The method can then be invoked on an instance of that type, omitting its first argument, so we end up with trs.TransformVectors(v), effectively asking a matrix to transform a vector. Change Shapes.Job to use this approach, eliminating its own version of the method.
//float4x3 TransformVectors (float3x4 trs, float4x3 p, float w = 1f) => float4x3(…);public void Execute (int i) { Point4 p = default(S).GetPoint4(i, resolution, invResolution); positions[i] = transpose(positionTRS.TransformVectors(p.positions)); float3x4 n = transpose(normalTRS.TransformVectors(p.normals, 0f)); normals[i] = float3x4€( normalize(n.c0), normalize(n.c1), normalize(n.c2), normalize(n.c3) ); }
Do the same with HashVisualization.HashJob.
//float4x3 TransformPositions (float3x4 trs, float4x3 p) => float4x3(…);public void Execute (int i) { float4x3 p = domainTRS.TransformVectors(transpose(positions[i])); … }
Let's add another extension method to MathExtensions, this time a Get3x4 method that extracts the float3x4 portion of a float4x4 matrix.
public static float3x4 Get3x4 (this float4x4 m) => float3x4€(m.c0.xyz, m.c1.xyz, m.c2.xyz, m.c3.xyz);
Use it to simplify Shapes.Job.ScheduleParallel.
public static JobHandle ScheduleParallel ( NativeArray<float3x4> positions, NativeArray<float3x4> normals, int resolution, float4x4 trs, JobHandle dependency//) {// float4x4 tim = transpose(inverse(trs));) => new Job<S> { positions = positions, normals = normals, resolution = resolution, invResolution = 1f / resolution, positionTRS = trs.Get3x4(), normalTRS = transpose(inverse(trs)).Get3x4() }.ScheduleParallel(positions.Length, resolution, dependency); //}
Lattice Noise
The type of noise that we will create in this tutorial is known as value noise. It is a specific type of lattice noise, which is noise based on a geometric lattice, typically a regular grid.
Generic Noise Job
Because there are different types and flavors of noise we will create a dedicated static Noise class, like we created one for shapes. Just like Shapes, it contains an interface and a generic Job struct type. In this case the interface is INoise, defining a GetNoise4 method that returns a vectorized float4 value with noise, given a set of positions and hashes.
using Unity.Burst;
using Unity.Collections;
using Unity.Jobs;
using Unity.Mathematics;
using static Unity.Mathematics.math;
public static class Noise {
public interface INoise {
float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash);
}
[BurstCompile(FloatPrecision.Standard, FloatMode.Fast, CompileSynchronously = true)]
public struct Job<N> : IJobFor where N : struct, INoise {}
}
The job has positions for input, noise for output, and also needs a hash and domain transformation matrix. Its Execute method invokes the GetNoise4 method of the noise, passing it the transformed positions and the hash.
public struct Job: IJobFor where N : struct, INoise { [ReadOnly] public NativeArray<float3x4> positions; [WriteOnly] public NativeArray<float4> noise; public SmallXXHash4 hash; public float3x4 domainTRS; public void Execute (int i) { noise[i] = default(N).GetNoise4( domainTRS.TransformVectors(transpose(positions[i])), hash ); } }
Finish by adding an appropriate ScheduleParallel method to the job and a corresponding delegate type to Noise.
public struct Job<N> : IJobFor where N : struct, INoise {
…
public static JobHandle ScheduleParallel (
NativeArray<float3x4> positions, NativeArray<float4> noise,
int seed, SpaceTRS domainTRS, int resolution, JobHandle dependency
) => new Job<N> {
positions = positions,
noise = noise,
hash = SmallXXHash.Seed(seed),
domainTRS = domainTRS.Matrix,
}.ScheduleParallel(positions.Length, resolution, dependency);
}
public delegate JobHandle ScheduleDelegate (
NativeArray<float3x4> positions, NativeArray<float4> noise,
int seed, SpaceTRS domainTRS, int resolution, JobHandle dependency
);
Partial Classes
The next step is to add code for our lattice noise to Noise, but instead of putting it all in the same C# file let's put the lattice-specific code in a separate file to keep things organized. This is possible by turning Noise into a partial class. This tells the compiler that there can be multiple files that contain parts of Noise.
public static partial class Noise { … }
Now create a new C# asset file and name it Noise.Lattice. This naming convention is not mandatory but makes it clear that the file contains the lattice portion of Noise. Inside it we again define the partial Noise class, this time introducing a Lattice1D struct type that implements INoise by initially always returning zero. We start with lattice noise in a single dimension to keep things simple, hence we name it Lattice1D.
using Unity.Mathematics;
using static Unity.Mathematics.math;
public static partial class Noise {
public struct Lattice1D : INoise {
public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash) {
return 0f;
}
}
}
It is now possible to schedule a job to create 1D lattice noise in NoiseVisualization.
…
using static Noise;
public class NoiseVisualization : Visualization {
…
protected override void UpdateVisualization (
NativeArray<float3x4> positions, int resolution, JobHandle handle
) {
Job<Lattice1D>.ScheduleParallel(
positions, noise, seed, domain, resolution, handle
).Complete();
noiseBuffer.SetData(noise.Reinterpret<float>(4 * 4));
}
}
1D Noise
The first step to create 1D noise in Lattice1D.GetNoise4 is to hash the integer X coordinates, retrieve their first bytes as floats, then convert that to the −1–1 range. To do this, first floor the coordinates, feed them to the hash, convert it to unsigned integers, mask the first byte, convert that to floating-point values, and then adjust the range.
public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash) {
int4 p = (int4)floor(positions.c0);
float4 v = (uint4)hash.Eat(p) & 255;
return v * (2f / 255f) - 1f;
}

This gets us isolated hash values that are constant for integer coordinates, ignoring the fractional part of the coordinates. To make the noise smooth and continuous we have to blend these values in between integer coordinates. The integer coordinates define the points of the lattice structure. In between these points are spans of empty space that we have to fill with a continuous noise signal. To make this possible we need to known both points on either side of a span.

We designate the point that we currently have as p0. The other point is one step further and will be known as point p1. If we visualize p1 instead of p0 then we'll get the same pattern as before, but shifted by a single lattice step.
int4 p0 = (int4)floor(positions.c0); int4 p1 = p0 + 1; float4 v = (uint4)hash.Eat(p1) & 255;

To fill the span between the lattice points we need to combine both values, which means that we'll have to convert hashes to floating-point values twice. To simplify code that needs bytes or floating-points values let's add two properties to SmallXXHash4, one to retrieve the first vectorized byte—designated as bytes A—and one to retrieve the same data but converted to a value in the 0–1 range.
public uint4 BytesA => (uint4)this & 255; public float4 Floats01A => (float4)BytesA * (1f / 255f);
Now we can easily retrieve 0–1 values for p0 and p1, add them, and then subtract 1 in GetNoise4. That gives us the average of the two lattice point values in the −1–1 range.
//float4 v = (uint4)hash.Eat(p0) & 255;return hash.Eat(p0).Floats01A + hash.Eat(p1).Floats01A - 1f;

The same can be achieved via linear interpolation of p0 and p1, using the lerp function with 0.5 as its third argument. Its result has to be doubled before subtracting 1.
return lerp(hash.Eat(p0).Floats01A, hash.Eat(p1).Floats01A, 0.5f) * 2f - 1f;
Finally, to create a continuous transition interpolate from p0 to p1 based on the fractional part of the lattice coordinates. It can be found by subtracting p0 from the coordinates. This gives us the interpolator value, which we'll refer to as t.
float4 t = positions.c0 - p0; return lerp(hash.Eat(p0).Floats01A, hash.Eat(p1).Floats01A, t) * 2f - 1f;

Let's also add properties for the other three bytes and their 0–1 versions to SmallXXHash4, which will be handy in the future.
public uint4 BytesA => (uint4)this & 255; public uint4 BytesB => ((uint4)this >> 8) & 255; public uint4 BytesC => ((uint4)this >> 16) & 255; public uint4 BytesD => (uint4)this >> 24; public float4 Floats01A => (float4)BytesA * (1f / 255f); public float4 Floats01B => (float4)BytesB * (1f / 255f); public float4 Floats01C => (float4)BytesC * (1f / 255f); public float4 Floats01D => (float4)BytesD * (1f / 255f);
2D Noise
At this point we have continuouos 1D noise, although it isn't smooth yet. Before worrying about smoothness let's first make a 2D variant while the noise is in its simplest form.
When considering only a single dimension, we needed to keep track of two lattice points and an interpolator value. Let's define a LatticeSpan4 struct type for this data. As it's only used for internal lattice noise calculations keep it private inside Noise, in the Noise.Lattice file.
struct LatticeSpan4 {
public int4 p0, p1;
public float4 t;
}
Next, add a static GetLatticeSpan4 method that gives us this data for a given set of 1D coordinates.
static LatticeSpan4 GetLatticeSpan4 (float4 coordinates) {
float4 points = floor(coordinates);
LatticeSpan4 span;
span.p0 = (int4)points;
span.p1 = span.p0 + 1;
span.t = coordinates - points;
return span;
}
This allows us to simplify Lattice1D.GetNoise4.
public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash) {
LatticeSpan4 x = GetLatticeSpan4(positions.c0);
return lerp(
hash.Eat(x.p0).Floats01A, hash.Eat(x.p1).Floats01A, x.t
) * 2f - 1f;
}
Introduce Lattice2D, initially as a duplicate of Lattice1D.
public struct Lattice1D : INoise { … }
public struct Lattice2D : INoise { … }
Adjust NoiseVisualization.UpdateVisualization so it uses the 2D version.
Job<Lattice2D>.ScheduleParallel( positions, noise, seed, domain, resolution, handle ).Complete();
Now adjust Lattice2D.GetNoise4 so it also gets the lattice span data for the Z dimension, then use that instead of X to calculate the noise.
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash) {
LatticeSpan4
x = GetLatticeSpan4(positions.c0), z = GetLatticeSpan4(positions.c2);
return lerp(hash.Eat(z.p0).Floats01A, hash.Eat(z.p1).Floats01A, z.t) * 2f - 1f;
}
This produces the same pattern as before, but now in the Z dimension instead of the X dimension. We could've also use the Y dimension, but that wouldn't produce a visible pattern for our XZ plane unless we rotated the domain.


To create a pattern that depends on both X and Z we have to take both dimensions into consideration, ultimately ending up with hash values for the four corners of a lattice square.
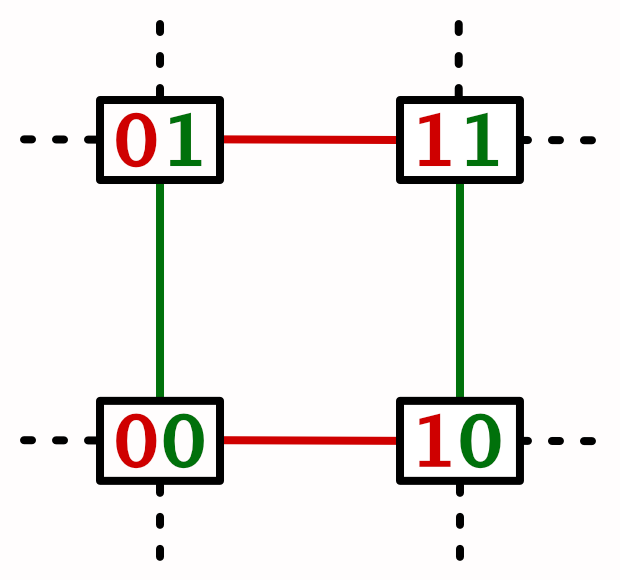
Let's initially calculate the hashes of the X points, referring to them as h0 and h1.
LatticeSpan4 x = GetLatticeSpan4(positions.c0), z = GetLatticeSpan4(positions.c2); SmallXXHash4 h0 = hash.Eat(x.p0), h1 = hash.Eat(x.p1);
Then feed the Z points to h0 instead of the original hash.
return lerp(h0.Eat(z.p0).Floats01A, h0.Eat(z.p1).Floats01A, z.t) * 2f - 1f;

As we now base our noise on both a single X point and the interpolation of two Z points we get continuous bands along the Z dimension, along with a discontinuous pattern along the X dimension. To complete the pattern we have to interpolate between the h0 and h1 bands along X as well. Thus we have to linearly interpolate two linear interpolations, which is known as bilinear interpolation.
return lerp( lerp(h0.Eat(z.p0).Floats01A, h0.Eat(z.p1).Floats01A, z.t), lerp(h1.Eat(z.p0).Floats01A, h1.Eat(z.p1).Floats01A, z.t), x.t ) * 2f - 1f;

Smooth Noise
Although we have a continuous 2D pattern it isn't smooth yet. The transitions through spans between the lattice points are straight flat segments, hence there is a sudden change in direction along the edges of the lattice squares. To make this smooth we need to take the rate of change of the noise into account. If we have a function, then its first derivative function describes its rate of change. As linear interpolation produces a straight line its derivative is a constant value. There is also a second derivative function, which is the derivative of the first derivative. You can think of it as the rate of change of the curvature, or the acceleration of the noise. In this case the second derivative is always zero.
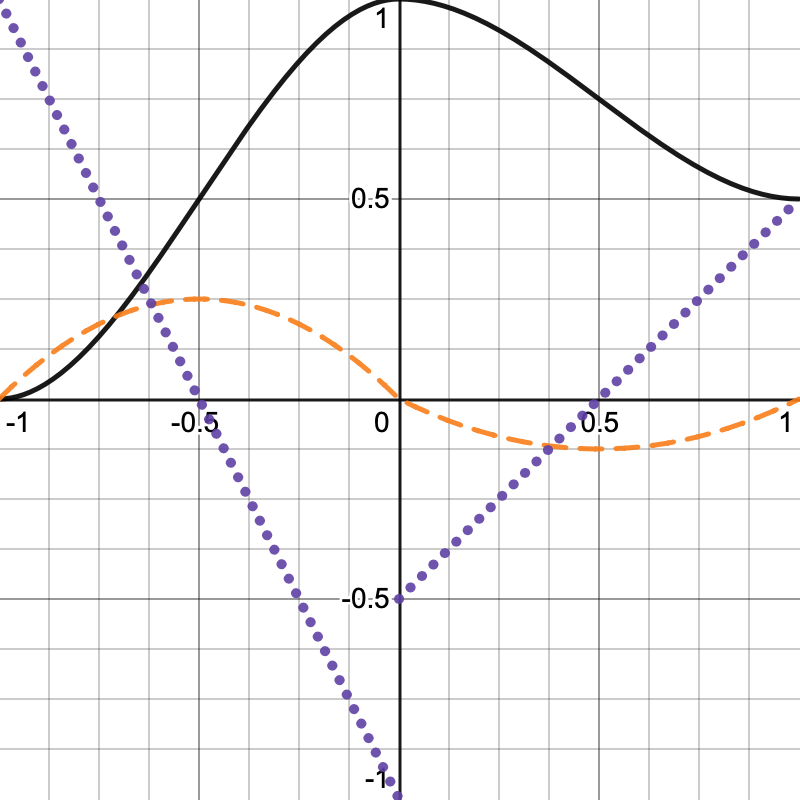
For example, in the below graph 1D noise is shown as a solid black line, its first derivative is a dashed orange line, and its second derivative is a dotted purple line. The derivatives are divided by 6 to scale them down so they're easier to see. Note that there is a discontinuity in the orange line at the lattice point in the middle, where the noise suddenly changes direction.
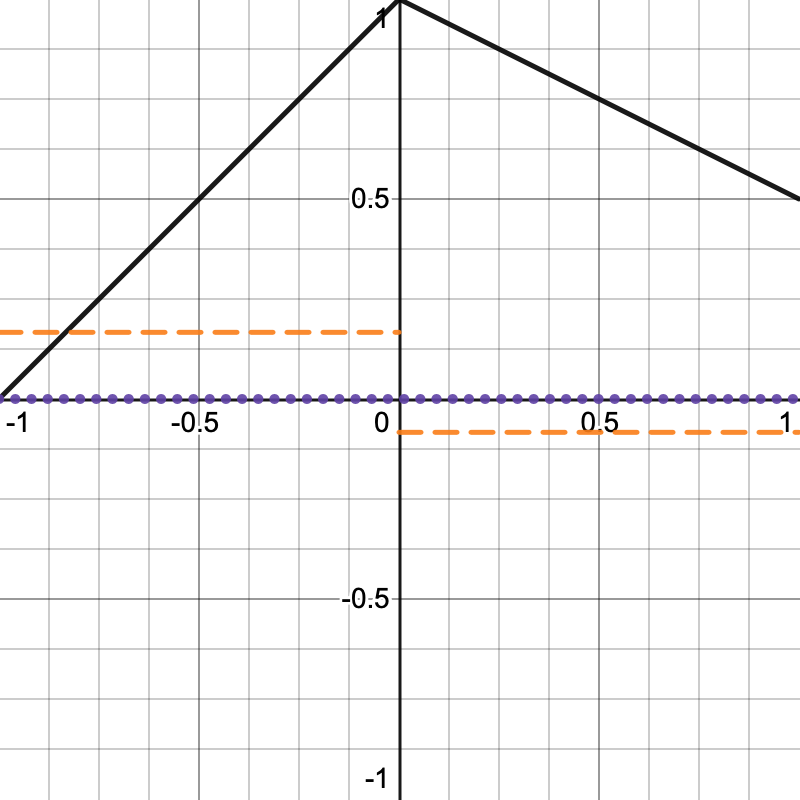
We can smooth that out by applying the smoothstep function to our interpolator in GetLatticeSpan4.
span.t = coordinates - points; span.t = smoothstep(0f, 1f, span.t);

This works because the smoothstep function—`3t^2-2t^3`—is horizontal for the inputs 0 and 1. This means that the first derivative of this function—`6t-6t^2`—is zero at both ends. It is known to be C1-continuous, while our linear interpolation was only C0-continuous. However, this isn't true for its second derivative—`6-12t`—so it isn't C2-continuous.
Second-Order Continuity
Although smoothstep is C1-continuous the derivative of this function is not continuous. This means that its rate of change can be different on both sides of a lattice edge. This isn't very noticeable when using our point-based visualization, but when the noise is used to define a smooth mesh surface or for a normal map, then this discontinuity can appear as visible creases revealing the lattice. To avoid this we have to go one step further, to a C2-continuous function, for which we can use `6t^5-15t^4+10t^3`. Its first derivative is `30t^4-60t^3+30t^2` and its second derivative is `120t^3-180t^2+60t`. Both derivatives yield zero for inputs 0 and 1.
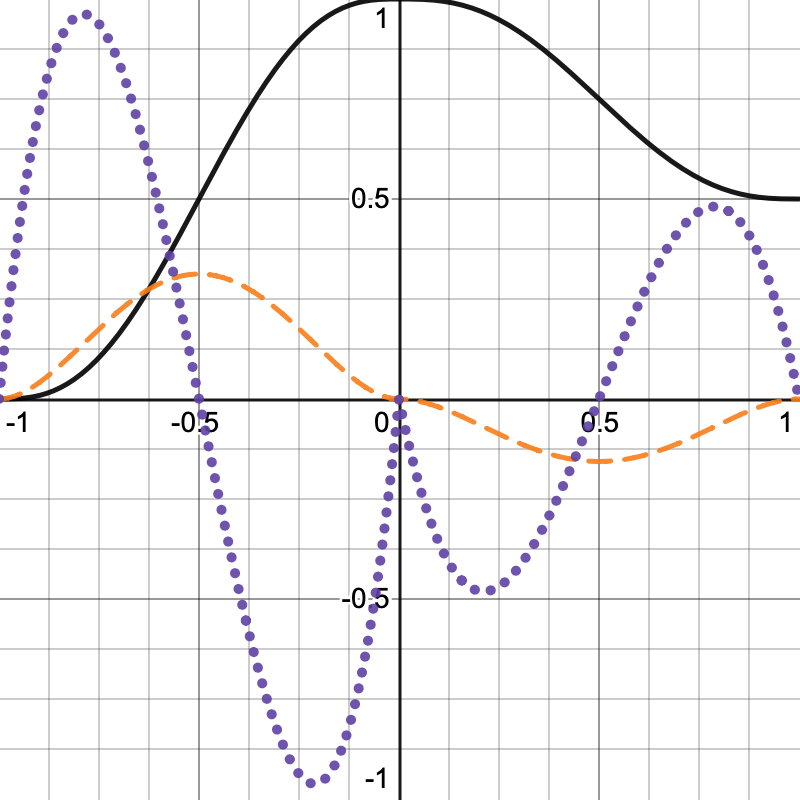
Adjust GetLatticeSpan4 to use this function. It can be rewritten to `t t t(t(t6-15)+10)`.
span.t = coordinates - points; span.t = span.t * span.t * span.t * (span.t * (span.t * 6f - 15f) + 10f);

3D Noise
We wrap up by adding the 3D version of value noise.
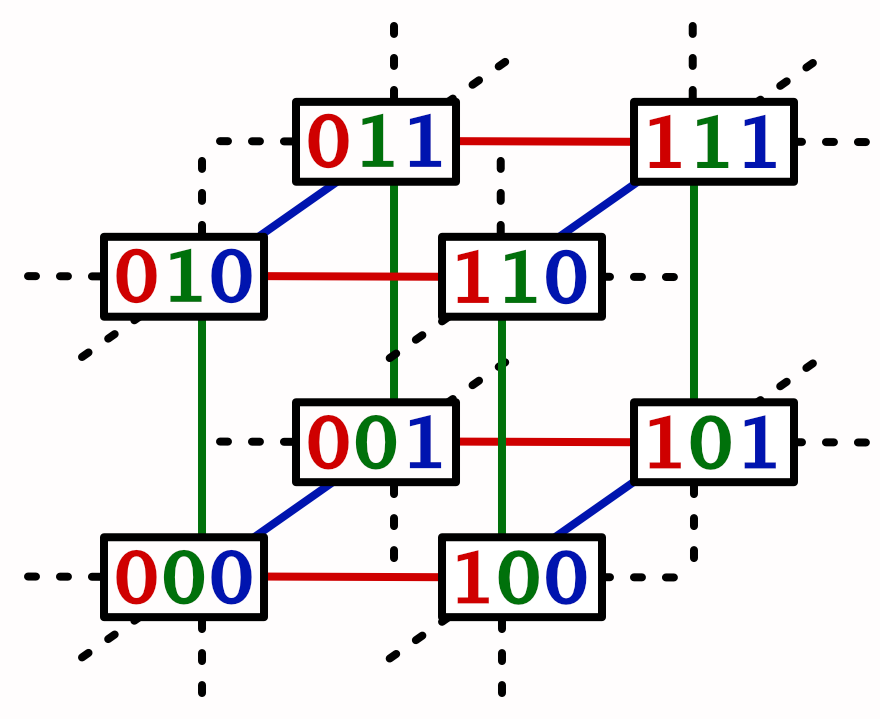
Create Lattice3D by duplicating Lattice2D and have it retrieve the lattice span data for the Y coordinates as well. Then also keep track of the hashes for the four points of the XY lattice square.
public struct Lattice3D : INoise {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash) {
LatticeSpan4
x = GetLatticeSpan4(positions.c0),
y = GetLatticeSpan4(positions.c1),
z = GetLatticeSpan4(positions.c2);
SmallXXHash4
h0 = hash.Eat(x.p0), h1 = hash.Eat(x.p1),
h00 = h0.Eat(y.p0), h01 = h0.Eat(y.p1),
h10 = h1.Eat(y.p0), h11 = h1.Eat(y.p1);
return lerp(…) * 2f - 1f;
}
}
Adjust the result so it interpolates between two YZ lattice squares along X.
return lerp( lerp( lerp(h00.Eat(z.p0).Floats01A, h00.Eat(z.p1).Floats01A, z.t), lerp(h01.Eat(z.p0).Floats01A, h01.Eat(z.p1).Floats01A, z.t), y.t ), lerp( lerp(h10.Eat(z.p0).Floats01A, h10.Eat(z.p1).Floats01A, z.t), lerp(h11.Eat(z.p0).Floats01A, h11.Eat(z.p1).Floats01A, z.t), y.t ), x.t ) * 2f - 1f;
Finally, add a configuration slider for the dimensions of the noise pattern to NoiseVisualization and use that to choose the correct version via a static array.
static ScheduleDelegate[] noiseJobs = {
Job<Lattice1D>.ScheduleParallel,
Job<Lattice2D>.ScheduleParallel,
Job<Lattice3D>.ScheduleParallel
};
…
[SerializeField, Range(1, 3)]
int dimensions = 3;
…
protected override void UpdateVisualization (
NativeArray<float3x4> positions, int resolution, JobHandle handle
) {
noiseJobs[dimensions - 1](
positions, noise, seed, domain, resolution, handle
).Complete();
noiseBuffer.SetData(noise.Reinterpret<float>(4 * 4));
}

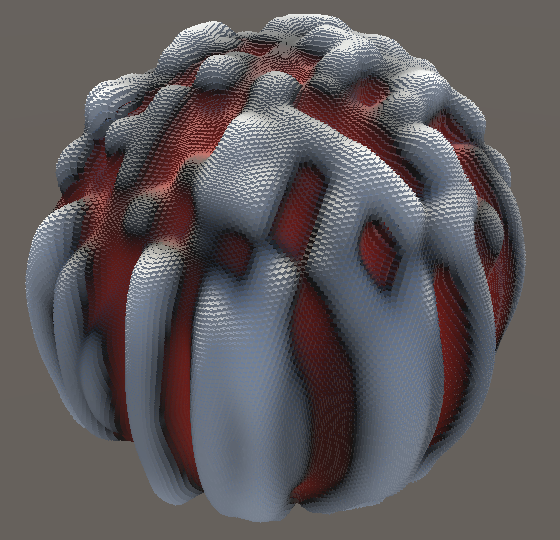
We can now quickly see the difference between the different versions of the noise. This is most obvious when using a 3D shape like the sphere.
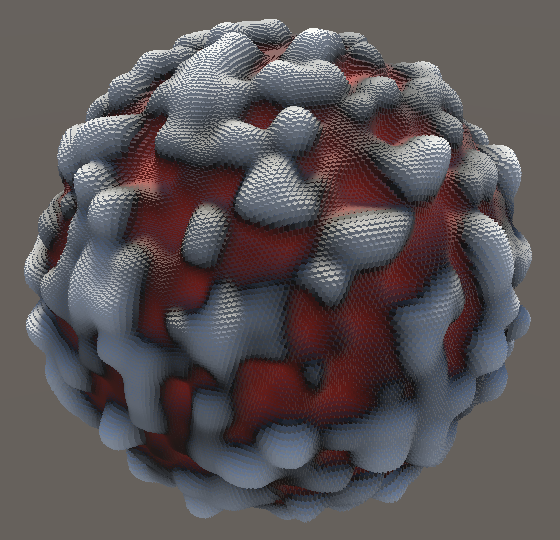

The next tutorial is Perlin Noise.