Voronoi Noise
Worley and Chebyshev
- Place cell points inside the lattice grid.
- Find the distance to the nearest point.
- Also find the distance to the second-nearest point.
- Support different functions and distance metrics.
This is the sixth tutorial in a series about pseudorandom noise. It introduces various flavors of Voronoi noise.
This tutorial is made with Unity 2020.3.12f1.
Distance to Nearest Point
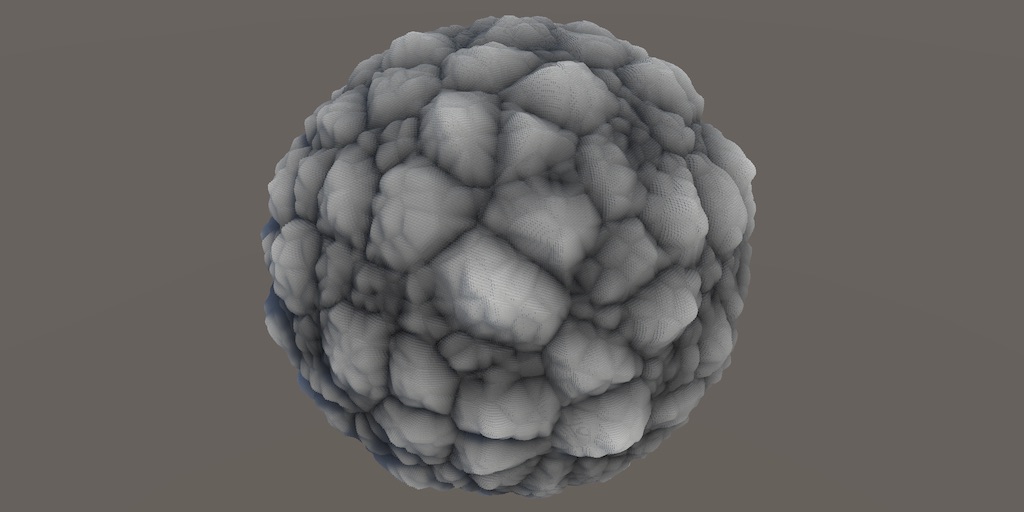
Besides value and gradient noise there is a third common type of noise. It is based on populating space with arbitrary points and finding the distance to the nearest point. The resulting pattern looks like a Voronoi diagram—space filled with convex polygonal cells—hence it is known as Voronoi or cell noise. This type of noise was first introduced by Steven Worley, hence it is also known as Worley noise.
Voronoi Noise Type
To support Voronoi noise we'll create a new partial Noise class in a separate Noise.Voronoi asset, containing 1D, 2D, and 3D implementations of INoise. Although it isn't technically lattice noise we'll use the lattice grid to generate the arbitrary points, so make all implementations use a generic ILattice to get lattice spans for all their dimensions. Besides that they'll all initially return zero.
using Unity.Mathematics;
using static Unity.Mathematics.math;
public static partial class Noise {
public struct Voronoi1D<L> : INoise where L : struct, ILattice {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
LatticeSpan4 x = default(L).GetLatticeSpan4(positions.c0, frequency);
return 0f;
}
}
public struct Voronoi2D<L> : INoise where L : struct, ILattice {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
LatticeSpan4
x = l.GetLatticeSpan4(positions.c0, frequency),
z = l.GetLatticeSpan4(positions.c2, frequency);
return 0f;
}
}
public struct Voronoi3D<L> : INoise where L : struct, ILattice {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
LatticeSpan4
x = l.GetLatticeSpan4(positions.c0, frequency),
y = l.GetLatticeSpan4(positions.c1, frequency),
z = l.GetLatticeSpan4(positions.c2, frequency);
return 0f;
}
}
}
To support visualizing the noise, add both regular and tiling versions of all Voronoi versions to the noise jobs array in NoiseVisualization.
static ScheduleDelegate[,] noiseJobs = {
{ … },
{ … },
{ … },
{ … },
{
Job<Voronoi1D<LatticeNormal>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling>>.ScheduleParallel
}
};
And include an entry for it in the NoiseType enum.
public enum NoiseType { Perlin€, PerlinTurbulence, Value€, ValueTurbulence, Voronoi }
1D Distances
We'll begin with the simplest case, which is 1D Voronoi noise. Like the other 1D noise types it isn't very useful, but it is easiest to understand so makes a good starting point.
The idea of Voronoi noise is that space is somehow filled with an arbitrary amount of points. The noise function is equal to the distance to the nearest point anywhere. Technically the amount of points to check is infinite, but we only need to know the nearest one. To make it possible to compute the noise we'll limit ourselves to a single arbitrary point per span.
Each span covers a single unit of space. We can put a point somewhere inside it by using Floats01A from the hash of that span. The distance from the sample position to that point is then equal to the absolute difference of their offsets inside the span. The sample offset inside the span is equal to g0, so subtract it from Floats01A and pass that through the abs method.
public struct Voronoi1D: INoise where L : struct, ILattice { public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) { LatticeSpan4 x = default(L).GetLatticeSpan4(positions.c0, frequency); SmallXXHash4 h = hash.Eat(x.p0); return abs(h.Floats01A - x.g0); } }

The result is a sequence of wedges or linear ramps, one per span, based on where inside each span the Voronoi point lies. The minimum of each ramp or wedge is always zero, which indicates the location of the Voronoi point. The maximum possible distance is 1, which is only reached if the Voronoi point lies on an edge of a span. So like the turbulence noise variants the amplitude range of the noise is 0–1.
Incorporating Adjacent Spans
The noise is currently discontinuous because we only consider the single point inside each span. But often a Voronoi point of an adjacent span lies closer to the sample position than the point inside the current span. So to get the correct distance we have to calculate the distances to the Voronoi points in the adjacent spans as well and pick the minimum.
To get the correct vectorized minima we have to invoke the select method. To make this convenient introduce a static vectorized UpdateVoronoiMinima method directly inside Noise.Voronoi. It takes the current minima and a new set of distances as input and returns the updated minima.
static float4 UpdateVoronoiMinima (float4 minima, float4 distances) {
return select(minima, distances, distances < minima);
}
Now change Voronoi1D.GetNoise4 so it loops through three spans with an offset of −1, 0, and 1, calculates the distance to the point in each span, and updates the minima each time. The initial minima before the loop must be invalid for this to work. As the theoretical maximum distance to the nearest point is 1 any greater initial value will do. Let's use 2.
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
LatticeSpan4 x = default(L).GetLatticeSpan4(positions.c0, frequency);
float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 h = hash.Eat(x.p0 + u);
minima = UpdateVoronoiMinima(minima, abs(h.Floats01A + u - x.g0));
}
return minima;
}

Now we have correct 1D Voronoi noise.
Tiling
A consequence of having to include adjacent spans in our calculations is that tiling no longer works, because the adjacent spans can extend beyond the tiling region.

To fix this we also have to apply tiling to the offset spans. Because we're either subtracting or adding 1 to the already tiled lattice coordinate, we only have to check two edge cases. We'll do both via a new ValidateSingleStep method signature that we add to the ILattice interface. It has the already-offset points and the frequency as parameters and returns the validated points. Note that the assumption of this method is that the input points are already correctly tiled and then had either −1, 0, or 1 added to them.
public interface ILattice {
LatticeSpan4 GetLatticeSpan4 (float4 coordinates, int frequency);
int4 ValidateSingleStep (int4 points, int frequency);
}
If we aren't tiling then the implementation of this method simply returns the same points.
public struct LatticeNormal : ILattice {
…
public int4 ValidateSingleStep (int4 points, int frequency) => points;
}
If tiling is used then there are two possible cases that need adjustment. First, if an offset point is equal to the frequency then it is now one step too far and has to loop back to zero.
public struct LatticeTiling : ILattice {
…
public int4 ValidateSingleStep (int4 points, int frequency) =>
select(points, 0, points == frequency);
}
Second, if an offset point is equal to −1 it has to loop to the maximum side, becoming equal to the frequency minus 1.
public int4 ValidateSingleStep (int4 points, int frequency) => select(select(points, 0, points == frequency), frequency - 1, points == -1);
Now we can make Voronoi1D.GetNoise4 tile correctly by passing the offset lattice point through ValidateSingleStep before feeding it to the hash inside the loop.
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
LatticeSpan4 x = l.GetLatticeSpan4(positions.c0, frequency);
float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 h = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
minima = UpdateVoronoiMinima(minima, abs(h.Floats01A + u - x.g0));
}
return minima;
}

2D Distances
To find the shortest distance in two dimensions we need to apply the Pythagorean theorem. Let's put a convenient static GetDistance method inside Noise.Voronoi to do this for two vectorized X and Y relative coordinate offsets.
static float4 GetDistance (float4 x, float4 y) => sqrt(x * x + y * y);
We begin the creation of 2D Voronoi noise by copying the loop for 1D noise and putting it inside Voronoi2D.GetNoise4.
public struct Voronoi2D<L> : INoise where L : struct, ILattice {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
LatticeSpan4
x = l.GetLatticeSpan4(positions.c0, frequency),
z = l.GetLatticeSpan4(positions.c2, frequency);
float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 h = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
minima = UpdateVoronoiMinima(minima, abs(h.Floats01A + u - x.g0));
}
return minima;
}
}
To incorporate the Z dimension we have to loop through it as well, once per X offset, so we end up with a nested loop, evaluating a total of nine lattice squares. Feed the offset Z lattice point to the hash and find the distance by applying both a X offset and a Z offset.
float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 hx = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
float4 xOffset = u - x.g0;
for (int v = -1; v <= 1; v++) {
SmallXXHash4 h = hx.Eat(l.ValidateSingleStep(z.p0 + v, frequency));
float4 zOffset = v - z.g0;
minima = UpdateVoronoiMinima(minima, GetDistance(
h.Floats01A + xOffset, h.Floats01D + zOffset
));
}
}
return minima;


2D Voronoi noise looks like a Voronoi diagram, with each cell containing a circular gradient increasing from zero at the cell's point to its maximum at the cell's edge. The edges are always equidistant from at least two cell points.
The maximum value of the noise is equal to the maximum distance that any sample point could be from a cell point. At its most extreme this is a sample point at the corner of a lattice square, with the nearest cell point in the diagonally opposite corner of the four cells surrounding the sample point. Hence the maximum amplitude of the noise is √2.
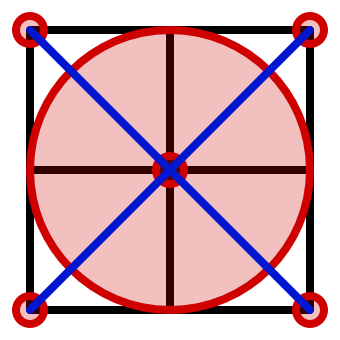
Although √2 is the theoretical maximum encountering it would be extremely rare. Most distances end up less than 1, but it is fairly common that they exceed 1. We can visualize this by returning the 1 threshold of the minima.
return select(0f, 1f, minima > 1f);


Two points per Lattice Square
A problem of allowing distances that exceed 1 is that it would mean that the nearest cell point could end up in a cell with an offset greater than one. We currently do not take this into consideration, which means that we have potential discontinuities in the noise, where adjacent lattice squares disagree about the nearest point.
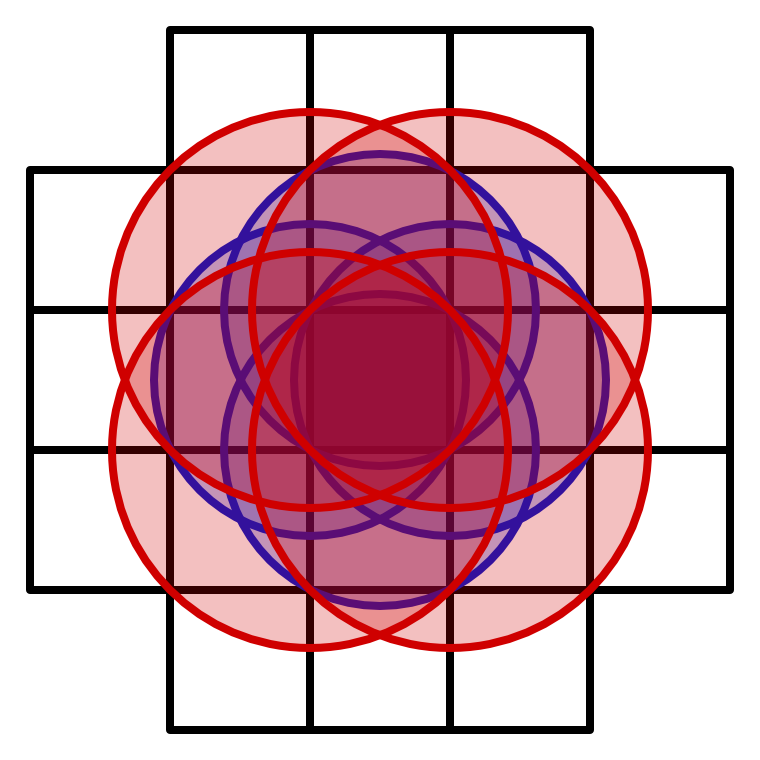
So the only way to guarantee artifact-free noise would be to evaluate up to 21 cells, which is not practical. However, this is only required when distances exceed one, which is uncommon. But we don't want the noise to exceed one, its range should be 0–1. So the practical solution is to clamp the noise so it never exceeds one.
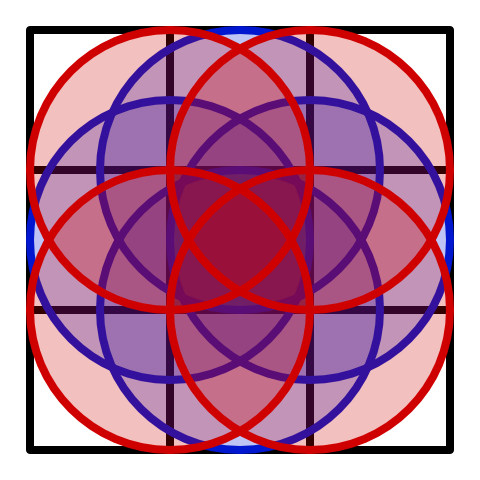
The downside of limiting the amplitude to 1 is that our noise will contain small regions where it becomes flat uniform 1. Although we cannot completely eliminate these regions we can make them extremely rare by increasing the amount of cell points per lattice square from one to two. We can do this by updating the minima twice per lattice square instead of just once, taking advantage of the fact that we can extract four values from the hash.
for (int u = -1; u <= 1; u++) {
SmallXXHash4 hx = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
float4 xOffset = u - x.g0;
for (int v = -1; v <= 1; v++) {
SmallXXHash4 h = hx.Eat(l.ValidateSingleStep(z.p0 + v, frequency));
float4 zOffset = v - z.g0;
minima = UpdateVoronoiMinima(minima, GetDistance(
h.Floats01A + xOffset, h.Floats01B + zOffset
));
minima = UpdateVoronoiMinima(minima, GetDistance(
h.Floats01C + xOffset, h.Floats01D + zOffset
));
}
}
return minima;


This makes the noise more compact and practically eliminates the flat regions. The final step is to guarantee that the final result never exceeds 1, in case we do encounter a flat region.
return min(minima, 1f);
3D Distances
The same approach to expand 1D noise to 2D noise can be used to create to 3D noise. Begin by introducing a 3D variant of the GetDistance method.
static float4 GetDistance (float4 x, float4 y, float4 z) => sqrt(x * x + y * y + z * z);
Then fill Voronoi3D.GetNoise4 with a triple loop, initially updating the minima once per lattice cube, thus 27 times.
public struct Voronoi3D<L> : INoise where L : struct, ILattice {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
LatticeSpan4
x = l.GetLatticeSpan4(positions.c0, frequency),
y = l.GetLatticeSpan4(positions.c1, frequency),
z = l.GetLatticeSpan4(positions.c2, frequency);
float4 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 hx = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
float4 xOffset = u - x.g0;
for (int v = -1; v <= 1; v++) {
SmallXXHash4 hy = hx.Eat(l.ValidateSingleStep(y.p0 + v, frequency));
float4 yOffset = v - y.g0;
for (int w = -1; w <= 1; w++) {
SmallXXHash4 h =
hy.Eat(l.ValidateSingleStep(z.p0 + w, frequency));
float4 zOffset = w - z.g0;
minima = UpdateVoronoiMinima(minima, GetDistance(
h.Floats01A + xOffset,
h.Floats01B + yOffset,
h.Floats01C + zOffset
));
}
}
}
return min(minima, 1f);
}
}


This gets us 3D Voronoi noise, which has the same problems as the 2D versions, but with a theoretical maximum amplitude of √3. We'll again drastically reduce the likelihood of the minima exceeding 1 by using two points per lattice cube. However, because we require three values to generate a cell point in 3D we need to extract six values from the hash in total. So the currently available A, B, C, and D values do not suffice.
Six Values Per Hash
We could add more explicit methods to SmallXXHash4 to support extracting six values from it, but that would clutter the class. So we'll instead give it general-purpose value extraction methods. The first is a GetBits method that returns a configurable amount of bits, shifted by a configurable amount of steps. The result is found by first right-shifting by the desired amount and then masking the result to limit it to the desired bit count. The mask is found by left-shifting 1 by the count and then subtracting one.
public uint4 GetBits (int count, int shift) => ((uint4)this >> shift) & (uint)((1 << count) - 1);
Also add an accompanying GetBitsAsFloats01 method that converts the bits to 0–1 values via a cast and appropriate scaling.
public float4 GetBitsAsFloats01 (int count, int shift) => (float4)GetBits(count, shift) * (1f / ((1 << count) - 1));
Two Points Per Lattice Cube
Now we can extract six values from the hash in Voronoi3D.GetNoise4. 32 divided by 6 rounded down equals 5, so we'll use five bits per coordinate, leaving 2 bits unused. This means that each coordinate has only `2^5=32` possible values instead of `2^8=256`, but that's still enough to create acceptable noise.
SmallXXHash4 h = hv.Eat(l.ValidateSingleStep(z.p0 + w, frequency)); float4 wOffset = w - z.g0; minima = UpdateVoronoiMinima(minima, GetDistance( h.GetBitsAsFloats01(5, 0) + xOffset, h.GetBitsAsFloats01(5, 5) + yOffset, h.GetBitsAsFloats01(5, 10) + zOffset )); minima = UpdateVoronoiMinima(minima, GetDistance( h.GetBitsAsFloats01(5, 15) + xOffset, h.GetBitsAsFloats01(5, 20) + yOffset, h.GetBitsAsFloats01(5, 25) + zOffset ));


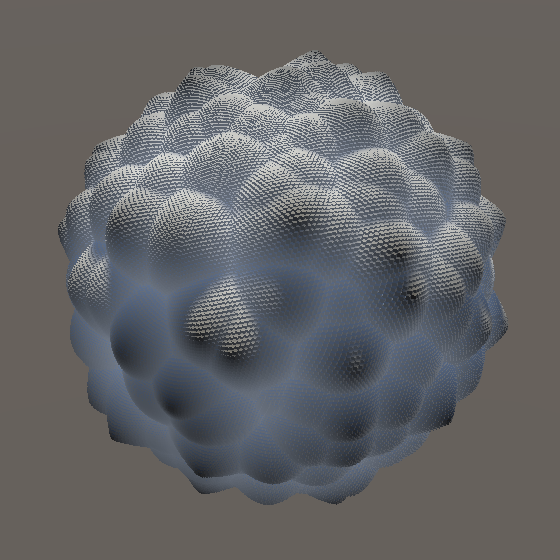
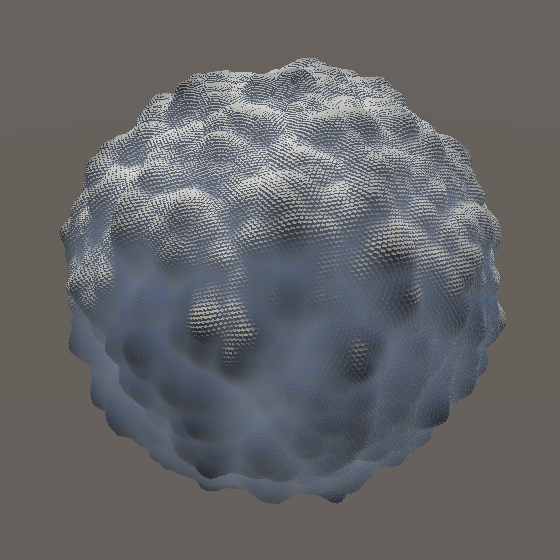
Note that when 3D Voronoi noise is projected on an axis-aligned plane it looks quite different than 2D Voronoi noise. The cell points from the 3D version most likely don't lie exactly on the plane, so the gradients inside most visible cells doesn't reach zero.


Distance to Second-Nearest Point
We don't need to limit ourselves to only considering the distance to the nearest cell point. There is also a second-nearest point, a third-nearest, and so on. Using those distances would produce different patterns. Of course distances to points further away are longer, so the average noise value will be higher and clamped flat regions will be more common. So we'll include the second-nearest distance only.
Tracking Two Minima
To find the second-nearest distance we also need to know the nearest distance, so we'll have to keep track of two minima per sample point instead of just one. Adjust UpdateVoronoiMinima so it accepts and return a float4x2 minima value. Its first vector contains the closest and its second vector contains the second-closest distances. This requires us to rewrite the code of this method, initially returning the minima unchanged.
static float4x2 UpdateVoronoiMinima (float4x2 minima, float4 distances) {
return minima;
}
The first step is to update the true minima as before, now contained in c0. Store the distance check for new minima in a boolean vector variable for convenience, as we'll have to check it twice for each minima vector.
static float4x2 UpdateVoronoiMinima (float4x2 minima, float4 distances) {
bool4 newMinimum = distances < minima.c0;
minima.c0 = select(minima.c0, distances, newMinimum);
return minima;
}
If there is a new minimum then the old minimum becomes the secondary minimum. So c1 has to be updated before c0.
bool4 newMinimum = distances < minima.c0; minima.c1 = select(minima.c1, minima.c0, newMinimum); minima.c0 = select(minima.c0, distances, newMinimum);
Besides that, it is also possible that a new distance doesn't provide a new primary minima but does provide a new secondary minima, so check for that as well.
minima.c1 = select( select(minima.c1, distances, distances < minima.c1), minima.c0, newMinimum );
We have to adjust Voronoi1D.GetNoise4 so it uses the new double-minima type. To keep the noise the same use c0 as the final result. This will produce the same code as before, as the unused secondary minima will be optimized away by Burst.
float4x2 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 h = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
minima = UpdateVoronoiMinima(minima, abs(h.Floats01A + u - x.g0));
}
return minima.c0;
Do the same for Voronoi2D and Voronoi3D.
float4x2 minima = 2f; … return min(minima.c0, 1f);
Voronoi Functions
The specific result that we use for Voronoi noise is usually known as its function. The function that shows the distance to the nearest cell point is named F1. The distance to the second-nearest point is named F2, and so on. To support easy application of these functions we'll introduce an IVoronoiFunction interface with a single Evaluate method that takes a double-minima vector and produces a single-vector result. Put it in a new Noise.Voronoi.Function partial Noise class asset.
using Unity.Mathematics;
public static partial class Noise {
public interface IVoronoiFunction {
float4 Evaluate (float4x2 minima);
}
}
Then add F1 and F2 structs that implement the interface, simply returning either c0 or c1.
public struct F1 : IVoronoiFunction {
public float4 Evaluate (float4x2 distances) => distances.c0;
}
public struct F2 : IVoronoiFunction {
public float4 Evaluate (float4x2 distances) => distances.c1;
}
The next step is to make the Voronoi structs use these functions. Add a generic type parameter for IVoronoiFunction to Voronoi1D and use it to evaluate the minima.
public struct Voronoi1D<L, F> : INoise
where L : struct, ILattice where F : struct, IVoronoiFunction {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
…
return default(F).Evaluate(minima);
}
}
Do the same for Voronoi2D, also clamping the minima vectors before evaluating the final result.
public struct Voronoi2D<L, F> : INoise
where L : struct, ILattice where F : struct, IVoronoiFunction {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
…
minima.c0 = min(minima.c0, 1f);
minima.c1 = min(minima.c1, 1f);
return default(F).Evaluate(minima);
}
}
Adjust Voronoi3D in the same way. Then adjust the job array in NoiseVisualization so it contains Voronoi versions for both F1 and F2.
{
Job<Voronoi1D<LatticeNormal, F1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, F1>>.ScheduleParallel
},
{
Job<Voronoi1D<LatticeNormal, F2>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, F2>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, F2>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, F2>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, F2>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, F2>>.ScheduleParallel
}
Finally, replace the single Voronoi element of NoiseType with two elements, for F1 and F2.
public enum NoiseType {
Perlin€, PerlinTurbulence, Value€, ValueTurbulence, VoronoiF1, VoronoiF2
}






The results of F2 show the same Voronoi cells as F1, but the directions of the gradients are reversed. Also, the cells are partitioned into gradients with different orientations, because different regions of a cell have different nearest cell neighbors.
F2 Minus F1
We don't have to limit ourselves to using either F1 or F2 exclusively, we can also use a function that combines them in some way. The most interesting variant is F2 − F1. Create an IVoronoiFunction for it in Noise.Voronoi.Function.
public struct F2MinusF1 : IVoronoiFunction {
public float4 Evaluate (float4x2 distances) => distances.c1 - distances.c0;
}
Add it to the job array in NoiseVisualization.
{
…
Job<Voronoi3D<LatticeTiling, F2>>.ScheduleParallel
},
{
Job<Voronoi1D<LatticeNormal, F2MinusF1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, F2MinusF1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, F2MinusF1>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, F2MinusF1>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, F2MinusF1>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, F2MinusF1>>.ScheduleParallel
}
And include it in NoiseType.
public enum NoiseType {
Perlin€, PerlinTurbulence, Value€, ValueTurbulence,
VoronoiF1, VoronoiF2, VoronoiF2MinusF1
}



F2 − F1 produces a strongly segmented pattern, which looks somewhat like angular cobblestones. This happens because F1 and F2 are equal along cell edges, while F2 always exceeds F1 inside cells. Thus the result is guaranteed to lie in the 0–1 range.
Note that this function doesn't produce perfect outlines. The strength of the gradient inside a cell depends on how close to a cell edge its point lies.
Distance Metrics
Besides changing the function of the Voronoi noise it is also possible to determine distances in different ways, because standard Euclidean distance isn't the only option.
Voronoi Distance Interface
To support multiple distance metrics we'll introduce the IVoronoiDistance interface, in a new Noise.Voronoi.Distance partial Noise class asset. Give it three GetDistance methods, for 1D, 2D, and 3D.
using Unity.Mathematics;
using static Unity.Mathematics.math;
public static partial class Noise {
public interface IVoronoiDistance {
float4 GetDistance (float4 x);
float4 GetDistance (float4 x, float4 y);
float4 GetDistance (float4 x, float4 y, float4 z);
}
}
Besides that, also include three finalization methods for the minima vectors, one per dimension. These will be invoked on the final minima and is where final clamping and other adjustments belong.
public interface IVoronoiDistance {
…
float4x2 Finalize1D (float4x2 minima);
float4x2 Finalize2D (float4x2 minima);
float4x2 Finalize3D (float4x2 minima);
}
Adjust Voronoi1D so it relies on a generic IVoronoiDistance type parameter. Use it to get the distance per span and to finalize the minima before evaluating them.
public struct Voronoi1D<L, D, F> : INoise
where L : struct, ILattice
where D : struct, IVoronoiDistance
where F : struct, IVoronoiFunction {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
var d = default(D);
LatticeSpan4 x = l.GetLatticeSpan4(positions.c0, frequency);
float4x2 minima = 2f;
for (int u = -1; u <= 1; u++) {
SmallXXHash4 h = hash.Eat(l.ValidateSingleStep(x.p0 + u, frequency));
minima =
UpdateVoronoiMinima(minima, d.GetDistance(h.Floats01A + u - x.g0));
}
return default(F).Evaluate(d.Finalize1D(minima));
}
}
Do this for Voronoi2D as well, also removing the clamping code from its GetNoise4 method.
public struct Voronoi2D<L, D, F> : INoise
where L : struct, ILattice
where D : struct, IVoronoiDistance
where F : struct, IVoronoiFunction {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
var d = default(D);
…
minima = UpdateVoronoiMinima(minima, d.GetDistance(
h.Floats01A + xOffset, h.Floats01B + zOffset
));
minima = UpdateVoronoiMinima(minima, d.GetDistance(
h.Floats01C + xOffset, h.Floats01D + zOffset
));
…
//minima.c0 = min(minima.c0, 1f);
//minima.c1 = min(minima.c1, 1f);
return default(F).Evaluate(d.Finalize2D(minima));
}
}
And do the same for Voronoi3D. Make sure that each noise version invokes the appropriate Finalize method.
public struct Voronoi3D<L, D, F> : INoise
where L : struct, ILattice
where D : struct, IVoronoiDistance
where F : struct, IVoronoiFunction {
public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
var l = default(L);
var d = default(D);
…
minima = UpdateVoronoiMinima(minima, d.GetDistance(
…
));
minima = UpdateVoronoiMinima(minima, d.GetDistance(
…
));
…
//minima.c0 = min(minima.c0, 1f);
//minima.c1 = min(minima.c1, 1f);
return default(F).Evaluate(d.Finalize3D(minima));
}
}
The static GetDistance methods are no longer needed after these changes, so remove them.
//static float4 GetDistance (float4 x, float4 y) => sqrt(x * x + y * y);//static float4 GetDistance (float4 x, float4 y, float4 z) =>// sqrt(x * x + y * y + z * z);
Voronoi Worley Noise
To make Voronoi noise work again we have to introduce a struct type that implements IVoronoiDistance in Noise.Voronoi.Distance, using the same Euclidean distance metrics and clamping that we have used up to this point. Because this is the default Voronoi noise implementation and it was introduced by Steven Worley let's name it Worley.
Because 2D and 3D finalization is the same Finalize3D can forward to Finalize2D, avoiding duplicate code.
public struct Worley : IVoronoiDistance {
public float4 GetDistance (float4 x) => abs(x);
public float4 GetDistance (float4 x, float4 y) => sqrt(x * x + y * y);
public float4 GetDistance (float4 x, float4 y, float4 z) =>
sqrt(x * x + y * y + z * z);
public float4x2 Finalize1D (float4x2 minima) => minima;
public float4x2 Finalize2D (float4x2 minima) {
minima.c0 = min(minima.c0, 1f);
minima.c1 = min(minima.c1, 1f);
return minima;
}
public float4x2 Finalize3D (float4x2 minima) => Finalize2D(minima);
}
Let's also introduce an optimization at this point. Because if `a<=b` then also `a^2<=b^2`—as long as `a` and `b` aren't negative—we can delay calculating the square root until finalization. This means that we only have to calculate square roots once instead of every iteration.
public float4 GetDistance (float4 x, float4 y) => x * x + y * y;
public float4 GetDistance (float4 x, float4 y, float4 z) => x * x + y * y + z * z;
public float4x2 Finalize2D (float4x2 minima) {
minima.c0 = sqrt(min(minima.c0, 1f));
minima.c1 = sqrt(min(minima.c1, 1f));
return minima;
}
Provide the new generic type argument in the job array of NoiseVisualization.
{
Job<Voronoi1D<LatticeNormal, Worley, F1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, Worley, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, Worley, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, Worley, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, Worley, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, Worley, F1>>.ScheduleParallel
},
And adjust the Voronoi labels to indicate that they represent the Worley variant.
public enum NoiseType {
Perlin€, PerlinTurbulence, Value€, ValueTurbulence,
VoronoiWorleyF1, VoronoiWorleyF2, VoronoiWorleyF2MinusF1
}
Voronoi Chebyshev Noise
We'll use chessboard distance as an alternative metric. It describes how many steps a king requires to reach a destination on a chess board. For a king diagonal movement is the same as axis-aligned movement. In general this means that the distance is equal to the maximum distance in any one dimension. This type of distance is commonly named after Pafnuty Chebyshev, so we'll name it Chebyshev.
Because of its nature the maximum possible distance is the same in all dimensions, so we do not need to limit the minima.
public struct Chebyshev : IVoronoiDistance {
public float4 GetDistance (float4 x) => abs(x);
public float4 GetDistance (float4 x, float4 y) => max(abs(x), abs(y));
public float4 GetDistance (float4 x, float4 y, float4 z) =>
max(max(abs(x), abs(y)), abs(z));
public float4x2 Finalize1D (float4x2 minima) => minima;
public float4x2 Finalize2D (float4x2 minima) => minima;
public float4x2 Finalize3D (float4x2 minima) => minima;
}
Add Chebyshev versions of Voronoi noise to the job array in NoiseVisualization.
{
…
Job<Voronoi3D<LatticeTiling, Worley, F2MinusF1>>.ScheduleParallel
},
{
Job<Voronoi1D<LatticeNormal, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, Chebyshev, F1>>.ScheduleParallel
},
{
Job<Voronoi1D<LatticeNormal, Chebyshev, F2>>.ScheduleParallel,
…
},
{
Job<Voronoi1D<LatticeNormal, Chebyshev, F2MinusF1>>.ScheduleParallel,
…
}
Before we continue, note that 1D Worley and Chebyshev noise are identical. So we can replace the entries for 1D Chebyshev noise with their Worley equivalents. The advantage of this is that Unity doesn't have to generate the 1D Chebyshev jobs.
{
Job<Voronoi1D<LatticeNormal, Worley, F1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, Worley, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi2D<LatticeTiling, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeNormal, Chebyshev, F1>>.ScheduleParallel,
Job<Voronoi3D<LatticeTiling, Chebyshev, F1>>.ScheduleParallel
},
{
Job<Voronoi1D<LatticeNormal, Worley, F2>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, Worley, F2>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, Chebyshev, F2>>.ScheduleParallel,
…
},
{
Job<Voronoi1D<LatticeNormal, Worley, F2MinusF1>>.ScheduleParallel,
Job<Voronoi1D<LatticeTiling, Worley, F2MinusF1>>.ScheduleParallel,
Job<Voronoi2D<LatticeNormal, Chebyshev, F2MinusF1>>.ScheduleParallel,
…
}
Finally, add the Chebyshev variants to NoiseType as well.
public enum NoiseType {
Perlin€, PerlinTurbulence, Value€, ValueTurbulence,
VoronoiWorleyF1, VoronoiWorleyF2, VoronoiWorleyF2MinusF1,
VoronoiChebyshevF1, VoronoiChebyshevF2, VoronoiChebyshevF2MinusF1
}








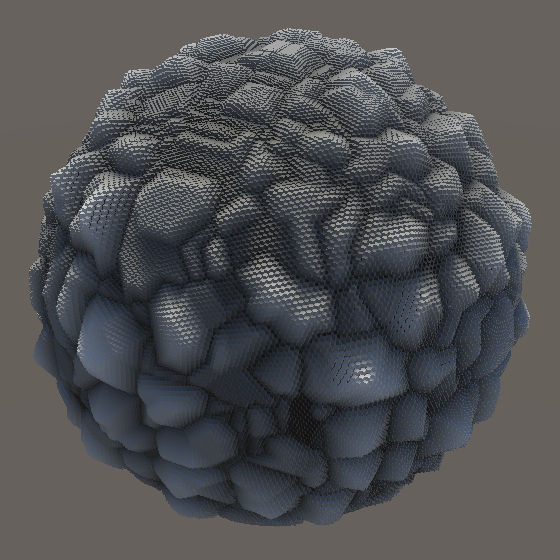
The cells of Chebyshev Voronoi noise have either diagonal or axis-aligned edges and their inner gradients form square patterns. This gives it an artificial look, compared to the more organic appearance of Worley noise. Also, an axis-aligned plane sampling 3D noise produces square regions of uniform color, wherever the closest point lies offset in the third dimension.
Other Metrics
There are other distance metrics that you could use. I'll mention three, but I won't include them in this tutorial.
The simplest variant is squared Euclidean distance, created by omitting the square root of the minima. This produces a similar pattern as Worley noise, but with a smaller average amplitude and weaker cell interiors. The advantage of this variant is that it's cheaper to calculate.


Another common variant is Manhattan distance, which disallows diagonal measurements. It corresponds to the movement of a rook on a chessboard. Thus the distance is the sum of the absolute distance in all dimensions. Its 2D version looks somewhat like Chebyshev rotated 45°. The downside of Manhattan is that the maximum 2D distance is 2 and the maximum 3D distance is 3, which means that there are many regions clamped to 1, especially for F2.


Finally, instead of producing distances it is also possible to visualize cell hashes. This works like our hash visualization, but based on Voronoi cells instead of the lattice grid. This requires adjusting our noise implementation to also generate an identifier value per cell point and keep track of the closest one. The cell identifier has to be extracted from the hash, cannibalizing bits from the values used to offset the point. For example, for 2D noise reduce the bits per coordinate offset to 6, so the remaining bits can be used for two 4-bit identifiers. For 3D noise the offsets have to be reduced to four bits each. Note that these identifiers can produce discontinuity artifacts in extremely rare cases when the true nearest cell lies outside the single-step offset region that we evaluate.


The next tutorial is Simplex Noise.