Mathematical Surfaces
Sculpting with Numbers
- Create a function library.
- Use a delegate and an enumeration type.
- Display 2D functions with a grid.
- Define surfaces in 3D space.
This is the third tutorial in a series about learning the basics of working with Unity. It is a continuation of the Building a Graph tutorial, so we won't start a new project. This time we'll make it possible to display multiple and more complex functions.
This tutorial is made with Unity 2020.3.6f1.
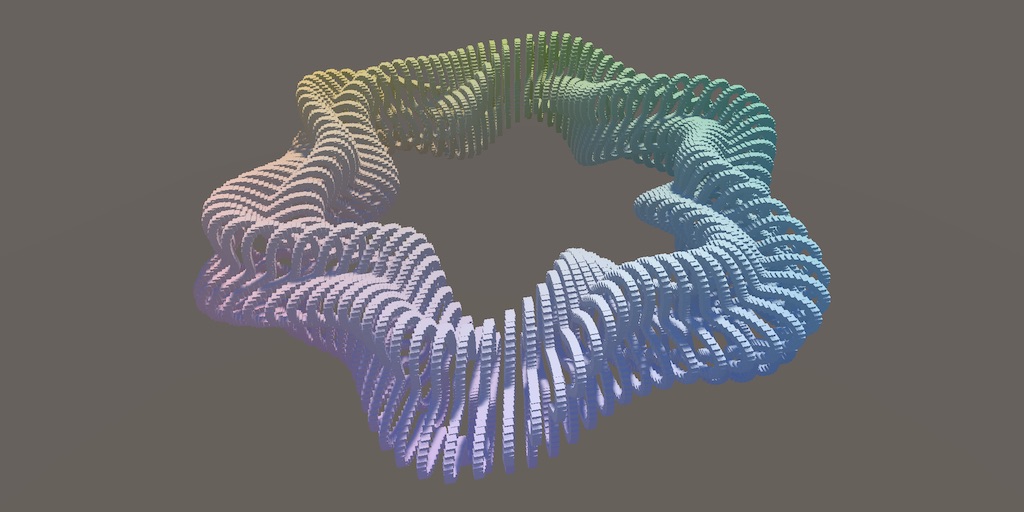
Function Library
After finishing the previous tutorial we have a point graph that shows an animated sine wave while in play mode. It is also possible to show other mathematical functions. You can change the code and the function will change along with it. You can even do this while the Unity editor is in play mode. Execution will be paused, the current game state saved, then the scripts are compiled again, and finally the game state is reloaded and play resumes. This is known as a hot reload. Not everything survives a hot reload, but our graph does. It will switch to animating the new function, without being aware that something changed.
While changing code during play mode can be convenient, it is not a handy way to switch back and forth between multiple functions. It would be much better if we could change the function via a configuration option of the graph.
Library Class
We could declare multiple mathematical functions inside Graph, but let's dedicate that class to displaying a function, leaving it unaware of the exact mathematical equations. This is an example of specialization and separation of concerns.
Create a new FunctionLibrary C# script and put it in the Scripts folder, next to Graph. You could either use a menu option to create a new asset or duplicate and the rename Graph. In either case clear the file contents and start with using UnityEngine and declaring an empty FunctionLibrary class that doesn't extend anything.
using UnityEngine;
public class FunctionLibrary {}
This class isn't going to be a component type. We're also not going to create an object instance of it. Instead we'll use it to provide a collection of publicly-accessible methods that represent math functions, similar to Unity's Mathf.
To signify that this class is not to be used as an object template mark it as static, by writing the static keyword before class.
public static class FunctionLibrary {}
Function Method
Our first function is going to be the same sine wave that Graph is currently showing. We need to create a method for it. This works the same as creating an Awake or Update method, except that we will name it Wave instead.
public static class FunctionLibrary {
void Wave () {}
}
By default methods are instance methods, which means that they have to be invoked on an object instance. To make them work directly at the class level we have to mark it as static, just like FunctionLibrary itself.
static void Wave () {}
And to make it publicly accessible give it the public access modifier as well.
public static void Wave () {}
This method is going to represent our mathematical function `f(x,t)=sin(pi(x+t))`. This means that it must produce a result, which has to be a floating-point number. So instead of void the return type of the function needs to be float.
public static float Wave () {}
Next, we have to add the two parameters to the method's parameter list, just like for the mathematical function. The only difference is that we have to write the type in front of each parameter, which is float.
public static float Wave (float x, float t) {}
Now we can put the code that computes the sine wave inside the method, using its x and t parameters.
public static float Wave (float x, float t) {
Mathf.Sin(Mathf.PI * (x + t));
}
The last step is to explicitly indicate what the result of the method is. As this is a float method, it has to return a float value when it's done. We indicate this by writing return followed by what the result is supposed to be, which is our mathematical computation.
public static float Wave (float x, float t) {
return Mathf.Sin(Mathf.PI * (x + t));
}
It is now possible to invoke this method inside Graph.Update, using position.x and time as arguments for its parameters. Its result can by used to set the point's Y coordinate, instead of an explicit math equation.
void Update () {
float time = Time.time;
for (int i = 0; i < points.Length; i++) {
Transform point = points[i];
Vector3 position = point.localPosition;
position.y = FunctionLibrary.Wave(position.x, time);
point.localPosition = position;
}
}
Implicitly using a Type
We'll be using Mathf.PI, Mathf.Sin, and other methods from Mathf at lot in FunctionLibrary. It would be nice if we could write those without having to explicitly mention the type all the time. We can make this possible by adding another using statement at the top of the FunctionLibrary file, with the extra static keyword followed by the explicit UnityEngine.Mathf type. That makes all constant and static members of the type usable without explicitly mentioning the type itself.
using UnityEngine;
using static UnityEngine.Mathf;
public static class FunctionLibrary { … }
Now we can shorten the code in Wave by omitting Mathf.
public static float Wave (float x, float z, float t) {
return Sin(PI * (x + t));
}
A Second Function
Let's add another function method. This time we'll make a slightly more complex function, using more than one sine wave. Begin by duplicating the Wave method and renaming it to MultiWave.
public static float Wave (float x, float t) {
return Sin(PI * (x + t));
}
public static float MultiWave (float x, float t) {
return Sin(PI * (x + t));
}
We'll keep the sine function that we already have, but add something extra to it. To make that easy, assign the current result to an y variable before returning it.
public static float MultiWave (float x, float t) {
float y = Sin(PI * (x + t));
return y;
}
The simplest way to add more complexity to a sine wave is to add another one that has double the frequency. This means that it changes twice as fast, which is done by multiplying the argument of the sine function by 2. At the same time, we'll halve the result of this function. That keeps the shape of the new sine wave the same as the old one, but at half size.
float y = Sin(PI * (x + t)); y += Sin(2f * PI * (x + t)) / 2f; return y;
This gives us the mathematical function `f(x,t)=sin(pi(x+t))+sin(2pi(x+t))/2`. As both the positive and negative extremes of the sine function are 1 and −1, the maximum and minimum values of this new function could be 1.5 and −1.5. To guarantee that we stay in the −1–1 range, we should divide the sum by 1.5.
return y / 1.5f;
Division requires a bit more work than multiplication, so it's a rule of thumb to prefer multiplication over division. However, constant expressions like 1f / 2f and also 2f * Mathf.PI are already reduced to a single number by the compiler. So we could rewrite our code to only use multiplication at runtime. We have to make sure that the constant portions are reduced first, using operation order and brackets.
y += Sin(2f * PI * (x + t)) * (1f / 2f); return y * (2f / 3f);
We can also directly write 0.5f instead of 1f / 2f, but the inverse of 1.5 cannot be written exactly in decimal notation so we'll keep using 2f / 3f, which the compiler reduces to a floating-point representation of it with maximum precision.
y += 0.5f * Sin(2f * PI * (x + t));
Now use this function instead of Wave in Graph.Update and see what it looks like.
position.y = FunctionLibrary.MultiWave(position.x, time);
You could say that a smaller sine wave is now following a larger sine wave. We can also make the smaller one slide along the larger, for example by halving the time for the larger wave. The result will be a function that doesn't just slide as time progresses, it changes its shape. It now takes four seconds for the pattern to repeat.
float y = Sin(PI * (x + 0.5f * t)); y += 0.5f * Sin(2f * PI * (x + t));
Selecting Functions in the Editor
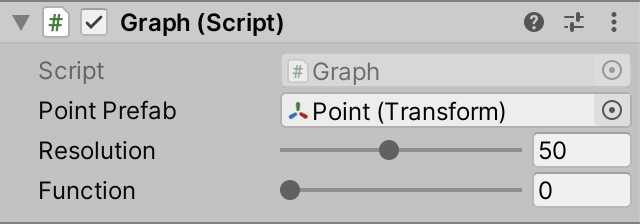
The next thing we can do is add some code that makes it possible to control which method is used by Graph. We could do this with a slider, just like for the graph's resolution. As we have two functions to choose from, we'll need a serializable integer field with a range of 0–1. Name it function so it's obvious what it controls.
[SerializeField, Range(10, 100)] int resolution = 10; [SerializeField, Range(0, 1)] int function;
Now we can check function inside the loop of Update. If it is zero then the graph should display Wave. To make that choice we'll use the if statement followed by an expression and a code block. This works like while except it doesn't loop back, so the block either gets executed or skipped. In this case the test is whether function equals zero, which can be done with the == equality operator.
void Update () {
float time = Time.time;
for (int i = 0; i < points.Length; i++) {
Transform point = points[i];
Vector3 position = point.localPosition;
if (function == 0) {
position.y = FunctionLibrary.Wave(position.x, time);
}
point.localPosition = position;
}
}
We can follow the if-block with else and another block, which gets executed if the test failed. In that case the graph should display MultiWave instead.
if (function == 0) {
position.y = FunctionLibrary.Wave(position.x, time);
}
else {
position.y = FunctionLibrary.MultiWave(position.x, time);
}
This makes it possible to control the function via the graph's inspector, also while we're in play mode.
Ripple Function
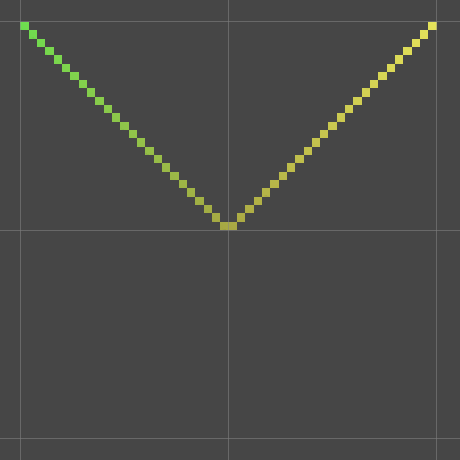
Let's add a third function to our library, one that produces a ripple-like effect. We create it by making a sine wave move away from the origin, instead of always traveling in the same direction. We can do this by basing it on the distance from the center, which is the absolute of X. Start with computing only that, with the help of Mathf.Abs, in a new FunctionLibrary.Ripple method. Store the distance in a d variable and then return it.
public static float Ripple (float x, float t) {
float d = Abs(x);
return d;
}
To show it, increase the range of Graph.function to 2 and add another block for the Wave method in Update. We can chain multiple conditional blocks by writing another if directly after else, so it becomes an else-if block which should be executed when function equals 1. Then add a new else block for the ripple.
[SerializeField, Range(0, 2)]
…
void Update () {
float time = Time.time;
for (int i = 0; i < points.Length; i++) {
Transform point = points[i];
Vector3 position = point.localPosition;
if (function == 0) {
position.y = FunctionLibrary.Wave(position.x, time);
}
else if (function == 1) {
position.y = FunctionLibrary.MultiWave(position.x, time);
}
else {
position.y = FunctionLibrary.Ripple(position.x, time);
}
point.localPosition = position;
}
}
Back to FunctionLibrary.Ripple, we use the distance as input for the sine function and make that the result. Specifically, we'll use `y=sin(4pid)` with `d=|x|` so the ripple goes up and down multiple times in the graph's domain.
public static float Ripple (float x, float t) {
float d = Abs(x);
float y = Sin(4f * PI * d);
return y;
}
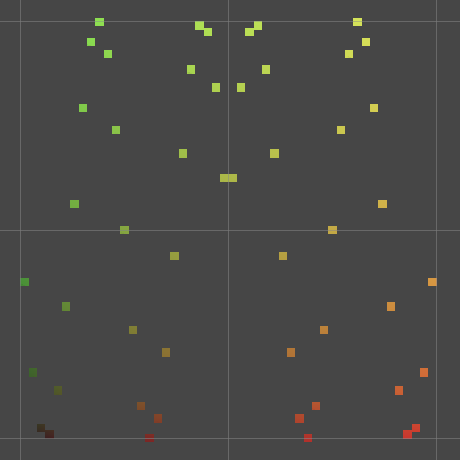
The result is visually hard to interpret because Y varies too much. We can reduce that by decreasing the amplitude of the wave. But a ripple doesn't have a fixed amplitude, it decreases with distance. So let's turn our function into `y=sin(4pid)/(1+10d)`.
float y = Sin(4f * PI * d); return y / (1f + 10f * d);
The finishing touch is animating the ripple. To make it flow outward we have to subtract the time from the value we pass to the sine function. Let's use `pit` so the final function becomes `y=sin(pi(4d-t))/(1+10d)`.
float y = Sin(PI * (4f * d - t)); return y / (1f + 10f * d);
Managing Methods
A sequence of conditional blocks works for two or three functions, but it gets unwieldy fast when trying to support more than that. It would be much more convenient if we could ask our library for a reference to a method based on some criteria and then invoke it repeatedly.
Delegates
It is possible to get a reference to a method by using a delegate. A delegate is a special type that defines what kind of method something can reference. There isn't a standard delegate type for our mathematical function methods, but we can define it ourselves. Because it is a type we could create it in its own file, but as it's specifically for methods of our library we'll define it inside the FunctionLibrary class, making it an inner or nested type.
To create the delegate type duplicate the Wave function, rename it to Function and replace its code block with a semicolon. This defines a method signature without an implementation. We then turn it into a delegate type by replacing the static keyword with delegate.
public static class FunctionLibrary {
public delegate float Function (float x, float t);
…
}
Now we can introduce a GetFunction method that returns a Function given an index parameter, using the same if-else logic that we used in the loop, except that in each block we return the appropriate method instead of invoking it.
public delegate float Function (float x, float t);
public static Function GetFunction (int index) {
if (index == 0) {
return Wave;
}
else if (index == 1) {
return MultiWave;
}
else {
return Ripple;
}
}
Next, we use this method to get a function delegate at the beginning of Graph.Update, based on function, and store it in a variable. Because this code isn't inside FunctionLibrary we have to refer to the nested delegate type as FunctionLibrary.Function.
void Update () {
FunctionLibrary.Function f = FunctionLibrary.GetFunction(function);
…
}
Then invoke the delegate variable instead of an explicit method in the loop.
for (int i = 0; i < points.Length; i++) {
Transform point = points[i];
Vector3 position = point.localPosition;
//if (function == 0) {
// position.y = FunctionLibrary.Wave(position.x, time);
//}
//else if (function == 1) {
// position.y = FunctionLibrary.MultiWave(position.x, time);
//}
//else {
// position.y = FunctionLibrary.Ripple(position.x, time);
//}
position.y = f(position.x, time);
point.localPosition = position;
}
An Array of Delegates
We've simplified Graph.Update a lot, but we only moved the if-else code to FunctionLibrary.GetFunction. We can get rid of this code completely by replacing it with indexing an array. Begin by adding a static field for a functions array to FunctionLibrary. This array is for internal use only, so don't make it public.
public delegate float Function (float x, float t);
static Function[] functions;
public static Function GetFunction (int index) { … }
We're always going to put the same elements in this array, so we can explicitly define its contents as part of its declaration. This is done by assigning a comma-separated array element sequence, between curly brackets. The simplest is an empty list.
static Function[] functions = {};
This means that we immediately get an array instance, but it is empty. Change this so it will contain delegates to our method, in the same order as before.
static Function[] functions = { Wave, MultiWave, Ripple };
The GetFunction method can now simply index the array to return the appropriate delegate.
public static Function GetFunction (int index) {
return functions[index];
}
Enumerations
An integer slider works, but it is not obvious that 0 represents the wave function and so on. It would be clearer if we had a dropdown list containing the function names. We can use an enumeration to achieve this.
Enumerations can be created by defining an enum type. Once again we'll do this inside FunctionLibrary, this time naming it FunctionName. In this case the type name is followed by a list of labels within curly brackets. We can use a copy of the array element list, but without the semicolon. Note that these are simple labels, they don't reference anything, although they follow the same rules as type names. It's our responsibility to keep the two lists identical.
public delegate float Function (float x, float t);
public enum FunctionName { Wave, MultiWave, Ripple }
static Function[] functions = { Wave, MultiWave, Ripple };
Now replace the index parameter of GetFunction with a name parameter of type FunctionName. This indicates that the argument has to be a valid function name.
public static Function GetFunction (FunctionName name) {
return functions[name];
}
Enumerations can be considered syntactical sugar. By default, each label of the enumeration represents an integer. The first label corresponds to 0, the second label to 1, and so on. So we can use the name to index the array. However, the compiler will complain that an enumeration cannot be implicitly cast to an integer. We have to explicitly perform this cast.
return functions[(int)name];
The last step is to change the type of the Graph.function field to FunctionLibrary.FunctionName and remove its Range attribute.
//[SerializeField, Range(0, 2)][SerializeField] FunctionLibrary.FunctionName function;
The inspector of Graph now shows a dropdown list containing the function names, with spaces added between capitalized words.
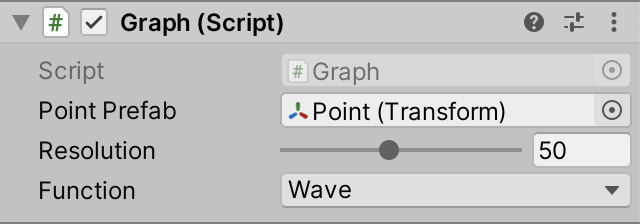
Adding Another Dimension
So far our graph only contains a single line of points. We map 1-dimensional values to other 1D values, though if you take time into account it's actually mapping 2D values to 1D values. So we're already mapping higher-dimensional input to a 1D value. Like we added time, we can add additional spatial dimensions as well.
Currently, we're using the X dimension as the spatial input for our functions. The Y dimension is used to display the output. That leaves Z as a second spatial dimension to use for input. Adding Z as an input upgrades our line to a square grid.
3D Colors
With Z no longer constant, change our Point Surface shader so it also modifies the blue albedo component, by removing the .rg and .xy code from the assignment.
surface.Albedo = saturate(input.worldPos * 0.5 + 0.5);
And adjust our Point URP shader graph so that Z is treated the same as X and Y.
Upgrading the Functions
To support a second non-time input for our functions, add a z parameter after the x parameter of the FunctionLibrary.Function delegate type.
public delegate float Function (float x, float z, float t);
This requires us to also add the parameter to our three function methods.
public static float Wave (float x, float z, float t) { … }
public static float MultiWave (float x, float z, float t) { … }
public static float Ripple (float x, float z, float t) { … }
And also add position.z as an argument when invoking the function in Graph.Update.
position.y = f(position.x, position.z, time);
Creating a Grid of Points
To show the Z dimension we have to turn our line of points into a grid of points. We can do this by creating multiple lines, each offset one step along Z. We'll use the same range for Z as we use for X, so we'll create as many lines as we currently have points. This means that we have to square the amount of points. Adjust the creation of the points array in Awake so it's big enough to contain all the points.
points = new Transform[resolution * resolution];
As we increase the X coordinate each iteration of the loop in Awake based on the resolution, simply creating more points will result in a single long line. We have to adjust the initialization loop to take the second dimension into account.

First, let's keep track of the X coordinate explicitly. Do this by declaring and incrementing an x variable inside the for loop, along with the i iterator variable. The third section of the for statement can be turned into a comma-separated lists for this purpose.
points = new Transform[resolution * resolution];
for (int i = 0, x = 0; i < points.Length; i++, x++) {
…
}
Each time we finish a row we have to reset x back to zero. A row is finished when x has become equal to resolution, so we can use an if block at the top of the loop to take care of this. Then use x instead of i to calculate the X coordinate.
for (int i = 0, x = 0; i < points.Length; i++, x++) {
if (x == resolution) {
x = 0;
}
Transform point = points[i] = Instantiate(pointPrefab);
position.x = (x + 0.5f) * step - 1f;
…
}
Next, each row has to be offset along the Z dimension. This can be done by adding a z variable to the for loop as well. This variable must not be incremented each iteration. Instead, it only increments when we move on to the next row, for which we already have an if block. Then set the position's Z coordinate just like its X coordinate, using z instead of x.
for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
if (x == resolution) {
x = 0;
z += 1;
}
Transform point = points[i] = Instantiate(pointPrefab);
position.x = (x + 0.5f) * step - 1f;
position.z = (z + 0.5f) * step - 1f;
…
}
We now create a square grid of points instead of a single line. Because our functions still only use the X dimension it will look like the original points have been extruded into lines.

Better Visuals
Because our graph is now 3D I'll be looking at it from a perspective viewpoint from now on, using the game window. To quickly choose a good camera position you can find a nice viewpoint in the scene window while in play mode, exit play mode and then make the game's camera match the viewpoint. You can do that via GameObject / Align With View with Main Camera selected and the scene window visible. I made it look roughly down on the XZ diagonal. Then I changed the Y rotation of Directional Light from −30 to 30, to improve the lighting for that view angle.
Besides that, we can tweak the shadow quality a bit. Shadows probably already look acceptable when using the default render pipeline, but they're configured for looking far away while we're looking at our graph up close.
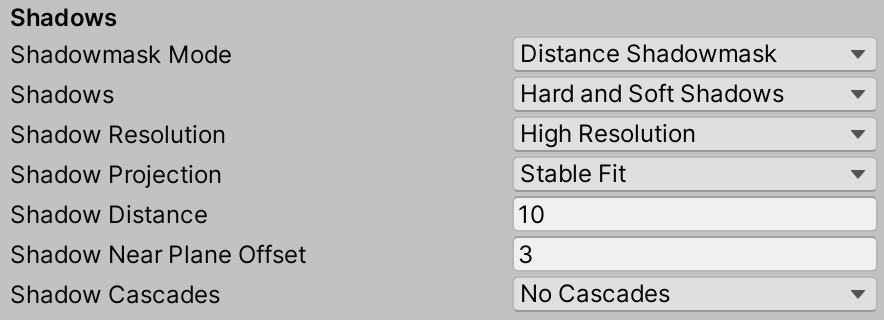
You can select the visual quality level for the default render pipeline by going to the Quality project settings and selecting one of the preconfigured levels. The default dropdown controls which level gets used by default for standalone apps.

We can tweak performance and precision of the shadows further by going to the Shadows section below and reducing Shadow Distance to 10 and setting Shadow Cascades to No Cascades. The default settings render shadows four times, which is overkill for us.

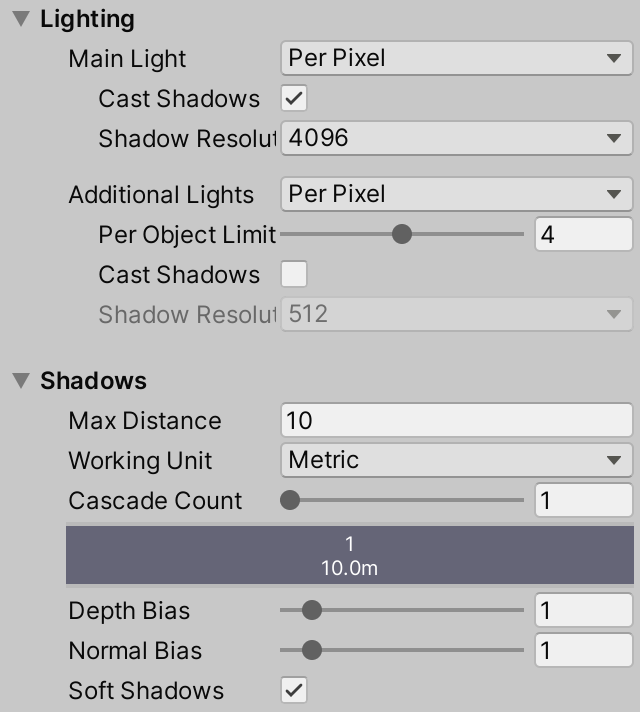
The URP doesn't use these settings, instead its shadows are configured via the inspector of our URP asset. It already renders directional shadows only once by default, but Shadows / Max Distance can be reduced to 10. Also, to match the standard Ultra quality of the default render pipeline enable Shadows / Soft Shadows and increase Lighting / Main Light / Shadow Resolution under Lighting to 4096.

Finally, you might notice visual tearing while in play mode. This can be prevented from happening in the game window by enabling VSync (Game view only) via the second dropdown menu from the left of the game window's toolbar. When enabled the presentation of new frames is synchronized with the display refresh rate. This only works reliably if no scene window is visible at the same time. VSync is configured for standalone apps via the Other section of the quality settings.

Incorporating Z
The simplest way to use Z in the Wave function is to use the sum of both X and Z instead of just X. That will create a diagonal wave.
public static float Wave (float x, float z, float t) {
return Sin(PI * (x + z + t));
}
And the most straightforward change for MultiWave is to make each wave use a separate dimension. Let's make the smaller one use Z.
public static float MultiWave (float x, float z, float t) {
float y = Sin(PI * (x + 0.5f * t));
y += 0.5f * Sin(2f * PI * (z + t));
return y * (2f / 3f);
}
We can also add a third wave that travels along the XZ diagonal. Let's use the same wave as Wave does, except with the time slowed down to a quarter. Then scale the result by dividing by 2.5 to keep it inside the −1–1 range.
float y = Sin(PI * (x + 0.5f * t)); y += 0.5f * Sin(2f * PI * (z + t)); y += Sin(PI * (x + z + 0.25f * t)); return y * (1f / 2.5f);
Note that the first and third waves will cancel each other out at regular intervals.
Finally, to make the ripple spread in all directions on the XZ plane we have to calculate the distance in both dimensions. We can use the Pythagorean theorem for this, with help of the Mathf.Sqrt method.
public static float Ripple (float x, float z, float t) {
float d = Sqrt(x * x + z * z);
float y = Sin(PI * (4f * d - t));
return y / (1f + 10f * d);
}
Leaving the Grid
By using X and Z to define Y we are able to create functions that describe a large variety of surfaces, but they're always linked to the XZ plane. No two points can have the same X and Z coordinates while having a different Y coordinate. This means that the curvature of our surfaces is limited. Their slopes cannot become vertical and they cannot fold backward. To make this possible, our functions would have to not only output Y, but also X and Z.
Three-Dimensional Functions
If our functions were to output 3D positions instead of 1D values we could use them to create arbitrary surfaces. For example, the function `f(x,z)=[[x],[0],[z]]` describes the XZ plane, while the function `f(x,z)=[[x],[z],[0]]` describes the XY plane.
Because the input parameters for these functions no longer have to correspond to the final X and Z coordinates, it's no longer appropriate to name them `x` and `z`. Instead, they're used to create a parametric surface and are often named `u` and `v`. So we'd get functions like `f(u,v)=[[u],[sin(pi(u+v))],[v]]`.
Adjust our Function delegate type to support this new approach. The only required change is replacing its float return type with Vector3, but let's also rename its parameters.
public delegate Vector3 Function (float u, float v, float t);
We also have to adjust our function methods accordingly. We'll simply use U and V directly for X and Z. It isn't required to adjust the parameter names—only their types need to match the delegate—but let's do this to stay consistent. If your code editor supports it you can quickly refactor-rename parameters and other things so it gets renamed everywhere it's used in one go, via a menu or context menu option.
Begin with Wave. Have it initially declare a Vector3 variable, then set its components, and then return it. We don't have to give the vector an initial value because we set all its fields before returning it.
public static Vector3 Wave (float u, float v, float t) {
Vector3 p;
p.x = u;
p.y = Sin(PI * (u + v + t));
p.z = v;
return p;
}
Then give MultiWave and Ripple the same treatment.
public static Vector3 MultiWave (float u, float v, float t) {
Vector3 p;
p.x = u;
p.y = Sin(PI * (u + 0.5f * t));
p.y += 0.5f * Sin(2f * PI * (v + t));
p.y += Sin(PI * (u + v + 0.25f * t));
p.y *= 1f / 2.5f;
p.z = v;
return p;
}
public static Vector3 Ripple (float u, float v, float t) {
float d = Sqrt(u * u + v * v);
Vector3 p;
p.x = u;
p.y = Sin(PI * (4f * d - t));
p.y /= 1f + 10f * d;
p.z = v;
return p;
}
Because the X and Z coordinates of points are no longer constant we can also no longer rely on their initial values in Graph.Update. We can solve this problem by replacing the loop in Update with the same one used in Awake, except that we can now directly assign the function result to the point's position.
void Update () {
FunctionLibrary.Function f = FunctionLibrary.GetFunction(function);
float time = Time.time;
float step = 2f / resolution;
for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
if (x == resolution) {
x = 0;
z += 1;
}
float u = (x + 0.5f) * step - 1f;
float v = (z + 0.5f) * step - 1f;
points[i].localPosition = f(u, v, time);
}
}
Note that we only need to recalculate v when z changes. This does require us to set its initial value before the start of the loop.
float v = 0.5f * step - 1f;
for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
if (x == resolution) {
x = 0;
z += 1;
v = (z + 0.5f) * step - 1f;
}
float u = (x + 0.5f) * step - 1f;
//float v = (z + 0.5f) * step - 1f;
points[i].localPosition = f(u, v, time);
}
Also note that because Update now uses the resolution, changing it while in play mode will deform the graph, stretching or squashing the grid into a rectangle.
We no longer need to initialize the positions in Awake, so we can make that method a lot simpler. We can suffice with setting only the scale and parent of the points.
void Awake () {
float step = 2f / resolution;
var scale = Vector3.one * step;
//var position = Vector3.zero;
points = new Transform[resolution * resolution];
for (int i = 0; i < points.Length; i++) {
//if (x == resolution) {
// x = 0;
// z += 1;
//}
Transform point = points[i] = Instantiate(pointPrefab);
//position.x = (x + 0.5f) * step - 1f;
//position.z = (z + 0.5f) * step - 1f;
//point.localPosition = position;
point.localScale = scale;
point.SetParent(transform, false);
}
}
Creating a Sphere
To demonstrate that we indeed are no longer limited to one point per (X, Z) coordinate pair, let's create a function that defines a sphere. Add a Sphere method to FunctionLibrary for this purpose. Also add an entry for it to the FunctionName enum and the functions array. Start with always returning a point at the origin.
public enum FunctionName { Wave, MultiWave, Ripple, Sphere }
static Function[] functions = { Wave, MultiWave, Ripple, Sphere };
…
public static Vector3 Sphere (float u, float v, float t) {
Vector3 p;
p.x = 0f;
p.y = 0f;
p.z = 0f;
return p;
}
The first step to creating a sphere is to describe a circle, laying flat in the XZ plane. We can use `[[sin(piu)],[0],[cos(piu)]]` for this, relying solely on `u`.
p.x = Sin(PI * u); p.y = 0f; p.z = Cos(PI * u);

We now have multiple circles that overlap perfectly. We can extrude them along Y based on `v`, which gives us an uncapped cylinder.
p.x = Sin(PI * u); p.y = v; p.z = Cos(PI * u);

We can adjust the radius of the cylinder by scaling X and Z by some value `r`. If we use `r=cos(pi/2v)` then the cylinder's top and bottom get collapsed to single points.
float r = Cos(0.5f * PI * v); Vector3 p; p.x = r * Sin(PI * u); p.y = v; p.z = r * Cos(PI * u);
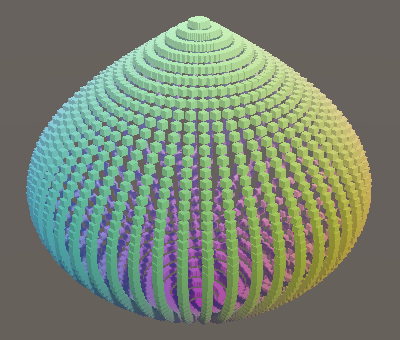
This gets us close to a sphere, but the reduction of the cylinder's radius isn't circular yet. That's because a circle is made with both a sine and a cosine, and we're only using the cosine for its radius at this point. The other part of the equation is Y, which is currently still equal to `v`. To complete the circle everywhere we have to use `y=sin(pi/2v)`.
p.y = Sin(PI * 0.5f * v);
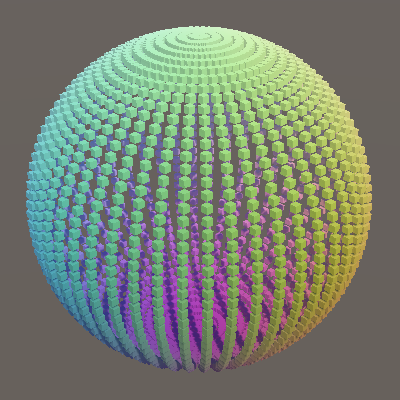
The result is a sphere, created with a pattern that's usually known as a UV-sphere. While this approach creates a correct sphere, note that the distribution of points isn't uniform, because the sphere is created by stacking circles with different radii. Alternatively, we can consider it to consists of multiple half-circles that are rotated around the Y axis.
Perturbing the Sphere
Let's tweak the surface of the sphere to make it more interesting. To do this we have to adjust our formula somewhat. We'll use `f(u,v)=[[ssin(piu)],[rsin(pi/2v)],[scos(piu)]]`, where `s=rcos(pi/2v)`, and `r` is the radius. That makes it possible to animate the radius. For example, we could animate it by using `r=(1+sin(pit))/2` to scale it based on time.
float r = 0.5f + 0.5f * Sin(PI * t); float s = r * Cos(0.5f * PI * v); Vector3 p; p.x = s * Sin(PI * u); p.y = r * Sin(0.5f * PI * v); p.z = s * Cos(PI * u);
We don't have to use a uniform radius. We could vary it based on `u`, like `r=(9+sin(8piu))/10`.
float r = 0.9f + 0.1f * Sin(8f * PI * u);

This gives the sphere the appearance of having vertical bands. We can switch to horizontal bands by using `v` instead of `u`.
float r = 0.9f + 0.1f * Sin(8f * PI * v);

And by using both we get twisting bands. Let's add time as well to make them rotate, finishing with `r=(9+sin(pi(6u+4v+t)))/10`.
float r = 0.9f + 0.1f * Sin(PI * (6f * u + 4f * v + t));
Creating a Torus
Let's wrap up by adding a torus surface to FunctionLibrary. Duplicate Sphere, rename it to Torus and set its radius to 1. Also update the names and function array.
public enum FunctionName { Wave, MultiWave, Ripple, Sphere, Torus }
static Function[] functions = { Wave, MultiWave, Ripple, Sphere, Torus };
…
public static Vector3 Torus (float u, float v, float t) {
float r = 1f;
float s = r * Cos(0.5f * PI * v);
Vector3 p;
p.x = s * Sin(PI * u);
p.y = r * Sin(0.5f * PI * v);
p.z = s * Cos(PI * u);
return p;
}
We can morph our sphere into a torus by pulling its vertical half-circles away from each other and turning them into full circles. Let's begin with by switching to `s=1/2+rcos(pi/2v)`.
float s = 0.5f + r * Cos(0.5f * PI * v);

This gives us half a torus, with only the outer portion of its ring accounted for. To complete the torus we have to use `v` to describe an entire circle instead of half a circle. That can be done by using `piv` instead of `pi/2v` in `s` and `y`.
float s = 0.5f + r * Cos(PI * v); Vector3 p; p.x = s * Sin(PI * u); p.y = r * Sin(PI * v); p.z = s * Cos(PI * u);
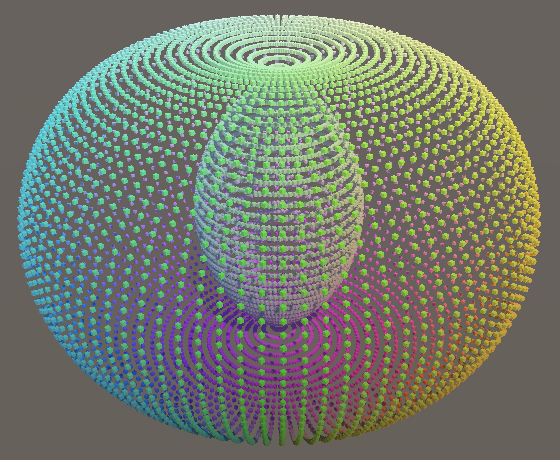
Because we've pulled the sphere apart by half a unit this produces a self-intersecting shape, known as a spindle torus. Had we pulled it apart by one unit instead, we would've gotten a torus that doesn't self-intersect, but doesn't have a hole either, which is known as a horn torus. So how far we pull the sphere apart influences the shape of the torus. Specifically, it defines the major radius of the torus. The other radius is the minor radius and determines the thickness of the ring. Let's define the major radius as `r_1` and rename the other to `r_2` so `s=r_2cos(piv)+r_1`. Then use 0.75 for the major and 0.25 for the minor radius to keep the points inside the −1–1 range.
//float r = 1f;float r1 = 0.75f; float r2 = 0.25f; float s = r1 + r2 * Cos(PI * v); Vector3 p; p.x = s * Sin(PI * u); p.y = r2 * Sin(PI * v); p.z = s * Cos(PI * u);

Now we have two radii to play with to make a more interesting torus. For example, we can turn it into a rotating star pattern by using `r_1=(7+sin(pi(6u+t/2)))/10`, while also twisting the ring by using `r_2=(3+sin(pi(8u+4v+2t)))/20`.
float r1 = 0.7f + 0.1f * Sin(PI * (6f * u + 0.5f * t)); float r2 = 0.15f + 0.05f * Sin(PI * (8f * u + 4f * v + 2f * t));
You now have some experience working with nontrivial functions that describe surfaces, plus how to visualize them. You can experiment with your own functions to get a better grasp of how it works. There are many seemingly complex parametric surfaces that can be created with a few sine waves.
The next tutorial is Measuring Performance.