Noise Variants

Fractals and Tiling

Combine multiple octaves of noise to create fractal patterns.
Introduce turbulence version of Perlin and value noise.
Add an option to create tiling noise.

This is the fifth tutorial in a series about pseudorandom noise. It adds fractal noise, turbulence, and tiling.

This tutorial is made with Unity 2020.3.12f1.

A torus showing six octaves of lacunarity 3 fractal 3D Perlin noise.

Fractal Noise

Up to this point we have only worked with a single sample of Perlin or value noise per point. The result appears random, but all features of the patterns have the same size. There is variety, but it is based on a uniform lattice. All variation exists at a single scale, determined by the domain transformation. The noise lacks variety at larger and smaller scales, which betrays its artificial nature.

We can introduce variety at a second frequency by sampling the noise again at a different scale. The simplest approach is to sample it at a base scale and also at double that scale. The sum of both samples produces a noise that has both large-scale and small-scale variety. We can do this multiply times, each extra sample at a larger domain scale adding smaller features. The resulting pattern would exhibit self-similarity as smaller features resemble larger features, thus the result is known as fractal noise.

Noise Settings

To support fractal noise we'll have to add some more configuration options to control it. To make it easy to pass the configuration to Noise we'll begin by creating a public Noise.Settings struct, initially only containing a seed integer field. As this struct is purely for conveniently grouping configuration options we make the field public and mark the struct as serializable with the System.Serializable attribute. That way Unity can save the configuration and it's easy to access its contents.

using System;
using Unity.Burst;
…

public static partial class Noise {

	[Serializable]
	public struct Settings {

		public int seed;
	}
	
	…
}

Struct fields cannot have default values other than zero or null, so we'll provide a default Settings configuration via a public static property. Initially it returns an unmodified new value, but we'll add field initializations to it later.

	public struct Settings {

		public int seed;

		public static Settings Default => new Settings {};
	}

Now adjust Noise.Job so it works with a Settings value instead of a hash directly. The hash is then intialized in Execute based on the configured seed.

		//public SmallXXHash4 hash;
		public Settings settings;

		public float3x4 domainTRS;

		public void Execute (int i) {
			var hash = SmallXXHash4.Seed(settings.seed);
			noise[i] = default(N).GetNoise4(
				domainTRS.TransformVectors(transpose(positions[i])), hash
			);
		}

		public static JobHandle ScheduleParallel (
			NativeArray<float3x4> positions, NativeArray<float4> noise, //int seed,
			Settings settings, SpaceTRS domainTRS, int resolution, JobHandle dependency
		) => new Job<N> {
			positions = positions,
			noise = noise,
			//hash = SmallXXHash.Seed(seed),
			settings = settings,
			domainTRS = domainTRS.Matrix,
		}.ScheduleParallel(positions.Length, resolution, dependency);

Adjust the delegate type to match the new signature of ScheduleParallel.

	public delegate JobHandle ScheduleDelegate (
		NativeArray<float3x4> positions, NativeArray<float4> noise, //int seed,
		Settings settings, SpaceTRS trs, int resolution, JobHandle dependency
	);

Finally, replace the seed configuration field of NoiseVisualization with a Settings field and pass that to the job instead.

	[SerializeField]
	//int seed;
	Settings noiseSettings = Settings.Default;

	…

	protected override void UpdateVisualization (
		NativeArray<float3x4> positions, int resolution, JobHandle handle
	) {
		noiseJobs[(int)type, dimensions - 1](
			positions, noise, noiseSettings, domain, resolution, handle
		).Complete();
		noiseBuffer.SetData(noise);
	}

Frequency

We're still only sampling the noise once per point. Currently the scale of the pattern is determined by the domain scale. This scale is also known as the frequency of the noise, which describes how fast it changes. The higher the frequency or scale, the faster it changes thus the smaller its features are.

We make it easier to adjust the frequency by adding a field for it to Settings. We restrict the frequency to whole numbers for reasons that will become clear later, so make it an integer. The frequency must be positive and at least one—enforced in the inspector via the Min attribute—and let's give it a default of 4.

…
using UnityEngine;

using static Unity.Mathematics.math;

public static partial class Noise {

	[Serializable]
	public struct Settings {

		public int seed;

		[Min(1)]
		public int frequency;

		public static Settings Default => new Settings {
			frequency = 4
		};
	}
	
	…
}

Frequency set to 4, domain scale set to 1.

To apply the frequency, use it to scale the transformed position in Noise.Job.Execute.

		public void Execute (int i) {
			float4x3 position = domainTRS.TransformVectors(transpose(positions[i]));
			var hash = SmallXXHash4.Seed(settings.seed);
			int frequency = settings.frequency;
			noise[i] = default(N).GetNoise4(frequency * position, hash);
		}

From now on both the frequency and the domain scale can be used to adjust the scale of the noise. The frequency is uniform, while the domains scale can be nonuniform and even negative per dimension.

Octaves

Fractal noise consists of multiple samples at different frequencies. These are known as octaves. Perfect fractal noise would have an infinite amount of octaves, but we'll have to calculate each octave separately so can only support a few. The more octaves there are the more details the noise has, but it also takes longer to generate. So we add an integer field to control the amount of octaves to Settings. There should be at least one octave and six is a reasonable maximum. A single octave is a good default.

		[Range(1, 6)]
		public int octaves;

		public static Settings Default => new Settings {
			frequency = 4,
			octaves = 1
		};

Now change Noise.Job.Execute so it loops over all octaves, invoking GetNoise4 each time and doubling the frequency afterwards. Sum all samples and use that for the final noise values.

		public void Execute (int i) {
			float4x3 position = domainTRS.TransformVectors(transpose(positions[i]));
			var hash = SmallXXHash4.Seed(settings.seed);
			int frequency = settings.frequency;
			float4 sum = 0f;

			for (int o = 0; o < settings.octaves; o++) {
				sum += default(N).GetNoise4(frequency * position, hash);
				frequency *= 2;
			}
			noise[i] = sum;
		}

I'll use screenshots of value noise to demonstrate the results because its blocky pattern makes the different octaves easier to spot than those of Perlin noise.

1 octave — One, two, and three octaves of 2D value noise.

2 octaves — One, two, and three octaves of 2D value noise.

When summing multiple octaves of the same strength the higher frequencies will dominate the result. The idea of fractal noise is that the amplitude of an octave decreases as its frequency increases. So each time we double the frequency we should also halve the amplitude of the noise.

			int frequency = settings.frequency;
			float amplitude = 1f;
			float4 sum = 0f;

			for (int o = 0; o < settings.octaves; o++) {
				sum += amplitude * default(N).GetNoise4(frequency * position, hash);
				frequency *= 2;
				amplitude *= 0.5f;
			}

Besides that, summing multiple octaves produces noise that goes outside the −1–1 range. So we should normalize the result, by dividing the octave sum by the sum of the amplitudes.

			float amplitude = 1f, amplitudeSum = 0f;
			float4 sum = 0f;

			for (int o = 0; o < settings.octaves; o++) {
				sum += amplitude * default(N).GetNoise4(frequency * position, hash);
				amplitudeSum += amplitude;
				frequency *= 2;
				amplitude *= 0.5f;
			}
			noise[i] = sum / amplitudeSum;

Unique Seeds Per Octave

We're currently summing the exact same noise pattern at different scales. A consequence of this is that at the domain origin the pattern appears to collapse into a singularity. Visually obvious repetition occurs at different scales, converging at the origin.

We can eliminate this visual artifact by using different hashes per octave. Incrementing the accumulator of SmallXXHash4 is enough for this, effectively using successive seeds per octave.

Add an addition operator method to SmallXXHash4 to support adding an integer value to the accumulator, which yields a different hash.

	public static SmallXXHash4 operator + (SmallXXHash4 h, int v) =>
		h.accumulator + (uint)v;

Then add the octave iterator value to the hash passed to GetNoise4 in the loop of Noise.Job.Execute.

				sum += amplitude * default(N).GetNoise4(frequency * position, hash + o);

Lacunarity

We don't always have to double the frequency between successive octaves. The frequency scaling is known as the lacunarity of the noise. Let's add an option for it to Settings, again as an integer, with a range of 2–4 and a default of 2.

		[Range(2, 4)]
		public int lacunarity;

		public static Settings Default => new Settings {
			frequency = 4,
			octaves = 1,
			lacunarity = 2
		};

To apply lacunarity use it to scale the frequency in Noise.Job.Execute instead of always doubling the frequency.

				sum += amplitude * default(N).GetNoise4(frequency * position, hash + o);
				frequency *= settings.lacunarity;
				amplitude *= 0.5f;
				amplitudeSum += amplitude;

lacunarity 2 — Lacunarity 2, 3, and 4; frequency 2 with three octaves.

lacunarity 3 — Lacunarity 2, 3, and 4; frequency 2 with three octaves.

Persistence

Just like lacunarity can be configurable instead of always being 2, so can the amplitude reduction between octaves be configurable instead of always being 0.5. This factor is known as persistence and controls how quickly the amplitude reduces per octave. It is a floating-point value in the 0–1 range. Add it to Settings with a default of 0.5.

		[Range(0f, 1f)]
		public float persistence;

		public static Settings Default => new Settings {
			frequency = 4,
			octaves = 1,
			lacunarity = 2,
			persistence = 0.5f
		};

Make Noise.Job.Execute apply persistence instead of always scaling the amplitude by 0.5.

				frequency *= settings.lacunarity;
				amplitude *= settings.persistence;

persistence 0.25 — Persistence 0.25, 0.5, and 0.75; frequency 4 with 3 octaves.

persistence 0.5 — Persistence 0.25, 0.5, and 0.75; frequency 4 with 3 octaves.

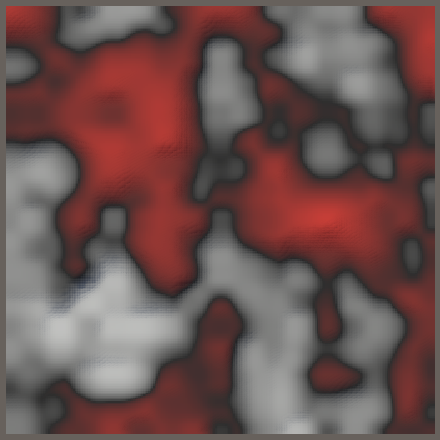
Turbulence

A common variant of fractal Perlin noise is to sum the absolute value of each octave. This causes the octaves to bounce where they would pass zero, creating a crease. Layering multiple such octaves produces a result that Ken Perlin described as a turbulent pattern, hence it is commonly known as the turbulence variant of Perlin noise. It can also be applied to value noise, so we will create turbulence variants of both noise types.

Evaluation After Interpolation

To take the absolute of an octave we have to perform an operation on the gradient noise value, after interpolation. We can generalize this to an arbitrary operation at this point, defined per gradient type. We do this by adding the signature for an EvaluateAfterInterpolation method to IGradient, which takes a vectorized noise value and evaluates it to yield the final post-interpolation noise value.

	public interface IGradient {
		float4 Evaluate (SmallXXHash4 hash, float4 x);

		float4 Evaluate (SmallXXHash4 hash, float4 x, float4 y);

		float4 Evaluate (SmallXXHash4 hash, float4 x, float4 y, float4 z);

		float4 EvaluateAfterInterpolation (float4 value);
	}

The regular Value and Perlin gradient implementations remain the same but still have to implement this method. They simply return the value unchanged.

	public struct Value : IGradient {

		…

		public float4 EvaluateAfterInterpolation (float4 value) => value;
	}

	public struct Perlin : IGradient {

		…

		public float4 EvaluateAfterInterpolation (float4 value) => value;
	}

To use the final evaluation pass the interpolated value through this new method at the end of GetNoise4. Do this for Lattice1D, Lattice2D, and Lattice3D.

			var g = default(G);
			return g.EvaluateAfterInterpolation(lerp(
				…
			));

Generic Turbulence

Now we can create turbulence variants of Perlin and value noise by duplicating them and changing their EvaluateAfterInterpolation method to return the absolute value. However, instead of duplicating both types let's introduce a generic Turbulence struct to Noise.Gradient that wraps an arbitrary other gradient type. It forwards all method invocations to the generic gradient, only changing the final evaluation to its absolute, via the abs method.

	public struct Turbulence<G> : IGradient where G : struct, IGradient {

		public float4 Evaluate (SmallXXHash4 hash, float4 x) =>
			default(G).Evaluate(hash, x);

		public float4 Evaluate (SmallXXHash4 hash, float4 x, float4 y) =>
			default(G).Evaluate(hash, x, y);

		public float4 Evaluate (SmallXXHash4 hash, float4 x, float4 y, float4 z) =>
			default(G).Evaluate(hash, x, y, z);

		public float4 EvaluateAfterInterpolation (float4 value) =>
			abs(default(G).EvaluateAfterInterpolation(value));
	}

Turbulence Perlin and Value Noise

We can now add turbulence variants to NoiseVisualization via the Turbulence<Perlin> and Turbulence<Value> gradient types. Add these to the noise jobs array, so we get regular Perlin noise followed by its turbulence versions, followed by the value versions in the same order.

	static ScheduleDelegate[,] noiseJobs = {
		{
			Job<Lattice1D<Perlin>>.ScheduleParallel,
			Job<Lattice2D<Perlin>>.ScheduleParallel,
			Job<Lattice3D<Perlin>>.ScheduleParallel
		},
		{
			Job<Lattice1D<Turbulence<Perlin>>>.ScheduleParallel,
			Job<Lattice2D<Turbulence<Perlin>>>.ScheduleParallel,
			Job<Lattice3D<Turbulence<Perlin>>>.ScheduleParallel
		},
		{
			Job<Lattice1D<Value>>.ScheduleParallel,
			Job<Lattice2D<Value>>.ScheduleParallel,
			Job<Lattice3D<Value>>.ScheduleParallel
		},
		{
			Job<Lattice1D<Turbulence<Value>>>.ScheduleParallel,
			Job<Lattice2D<Turbulence<Value>>>.ScheduleParallel,
			Job<Lattice3D<Turbulence<Value>>>.ScheduleParallel
		}
	};

Add them to the NoiseType enum as well, so they can be selected via the inspector.

	public enum NoiseType { Perlin€, PerlinTurbulence, Value€, ValueTurbulence }

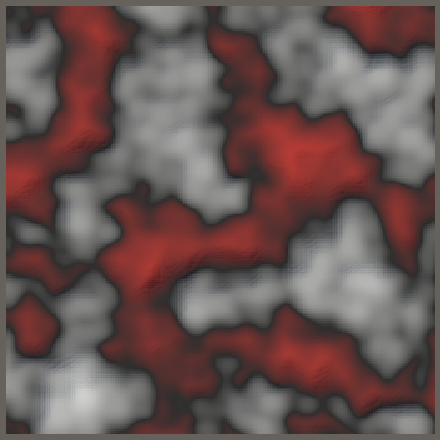
Perlin regular — Regular Perlin and value noise, and their turbulence variants.

value regular — Regular Perlin and value noise, and their turbulence variants.

Because absolute values are never negative the turbulence patterns are always grayscale and aren't centered on zero. A positive displacement looks quite different than a negative displacement. Positive has round peaks with narrow valleys, while negative has sharp ridges with wide valleys. In contrast, regular noise appears similar with both positive and negative displacement, only the orientation of the color gradient is different.

regular positive — Sphere with 0.2 and −0.2 displacement, both regular 3D Perlin and turbulence variant.

regular negative — Sphere with 0.2 and −0.2 displacement, both regular 3D Perlin and turbulence variant.

Tiling Noise

Another useful noise variant is one that creates repeating patterns. This isn't meant for filling a large area directly, but for generating a small texture or mesh that can then be used to seamlessly tile a larger area.

In order for a pattern to tile, opposite sides of the sample area must be identical. As we're using a lattice grid we can do this by repeating the same sequence of lattice spans. We make the length of this sequence equal to the noise frequency. So frequency 4 noise would repeat every four spans in any dimension.

To make this tiling possible the frequency and thus also the lacunarity must always be whole numbers, which is why we made them integers.

Frequency at the Lattice Level

To make repetition possible we have to pass the frequency to the noise implementation, so add a parameter for it to INoise.GetNoise4.

	public interface INoise {
		float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency);
	}

We'll apply the frequency at this lower level from now on, so pass it the unmodified position along with the frequency in Noise.Job.Evaluate instead of scaling the position in the loop.

				sum += amplitude * default(N).GetNoise4(position, hash + o, frequency);

The lattice points are determined in GetLatticeSpan4, so add a frequency parameter to it and scale the coordinates at the beginning of that method.

	static LatticeSpan4 GetLatticeSpan4 (float4 coordinates, int frequency) {
		coordinates *= frequency;
		float4 points = floor(coordinates);
		…
	}

The final step of this adjustment is adding the frequency parameter to the GetNoise4 methods of the lattice structs, passing it along to all invocations of GetLatticeSpan4.

	public struct Lattice1D<G> : INoise where G : struct, IGradient {

		public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash, int frequency) {
			LatticeSpan4 x = GetLatticeSpan4(positions.c0, frequency);

			…
		}
	}

	public struct Lattice2D<G> : INoise where G : struct, IGradient {

		public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
			LatticeSpan4
				x = GetLatticeSpan4(positions.c0, frequency),
				z = GetLatticeSpan4(positions.c2, frequency);

			…
		}
	}

	public struct Lattice3D<G> : INoise where G : struct, IGradient {

		public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
			LatticeSpan4
				x = GetLatticeSpan4(positions.c0, frequency),
				y = GetLatticeSpan4(positions.c1, frequency),
				z = GetLatticeSpan4(positions.c2, frequency);

			…
		}
	}

Lattice Interface

To support both normal and tiling noise we'll introduce a new ILattice interface in Noise.Lattice that specifies the GetLatticeSpan4 method signature. This requires the LatticeSpan4 struct to become public, as the method as a whole has to be public, including the types of its parameters and what it returns.

	public struct LatticeSpan4 { … }

	public interface ILattice {
		LatticeSpan4 GetLatticeSpan4 (float4 coordinates, int frequency);
	}

Now wrap the GetLatticeSpan4 method inside a new LatticeNormal struct type that implements ILattice, changing it to a public instance method.

	public struct LatticeNormal : ILattice {

		public LatticeSpan4 GetLatticeSpan4 (float4 coordinates, int frequency) {
			…
		}
	}

Then adjust the lattice struct types so they rely on a generic ILattice type to get their lattice spans. This means that they now have two generic type parameters. The generic type constraints are written one after the other.

	public struct Lattice1D<L, G> : INoise
		where L : struct, ILattice where G : struct, IGradient {

		public float4 GetNoise4(float4x3 positions, SmallXXHash4 hash, int frequency) {
			LatticeSpan4 x = default(L).GetLatticeSpan4(positions.c0, frequency);

			…
		}
	}

	public struct Lattice2D<L, G> : INoise
		where L : struct, ILattice where G : struct, IGradient {

		public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
			var l = default(L);
			LatticeSpan4
				x = l.GetLatticeSpan4(positions.c0, frequency),
				z = l.GetLatticeSpan4(positions.c2, frequency);

			…
		}
	}

	public struct Lattice3D<L, G> : INoise
		where L : struct, ILattice where G : struct, IGradient {

		public float4 GetNoise4 (float4x3 positions, SmallXXHash4 hash, int frequency) {
			var l = default(L);
			LatticeSpan4
				x = l.GetLatticeSpan4(positions.c0, frequency),
				y = l.GetLatticeSpan4(positions.c1, frequency),
				z = l.GetLatticeSpan4(positions.c2, frequency);

			…
		}
	}

We're now required to make explicit that we're using the normal lattice versions in NoiseVisualization, by providing the extra type argument in the noise jobs array.

	static ScheduleDelegate[,] noiseJobs = {
		{
			Job<Lattice1D<LatticeNormal, Perlin>>.ScheduleParallel,
			Job<Lattice2D<LatticeNormal, Perlin>>.ScheduleParallel,
			Job<Lattice3D<LatticeNormal, Perlin>>.ScheduleParallel
		},
		{
			Job<Lattice1D<LatticeNormal, Turbulence<Perlin>>>.ScheduleParallel,
			Job<Lattice2D<LatticeNormal, Turbulence<Perlin>>>.ScheduleParallel,
			Job<Lattice3D<LatticeNormal, Turbulence<Perlin>>>.ScheduleParallel
		},
		{
			Job<Lattice1D<LatticeNormal, Value>>.ScheduleParallel,
			Job<Lattice2D<LatticeNormal, Value>>.ScheduleParallel,
			Job<Lattice3D<LatticeNormal, Value>>.ScheduleParallel
		},
		{
			Job<Lattice1D<LatticeNormal, Turbulence<Value>>>.ScheduleParallel,
			Job<Lattice2D<LatticeNormal, Turbulence<Value>>>.ScheduleParallel,
			Job<Lattice3D<LatticeNormal, Turbulence<Value>>>.ScheduleParallel
		}
	};

Tiling

To create a tiling lattice, duplicate LatticeNormal and rename it to LatticeTiling. Then adjust its GetLatticeSpan4 method so it repeats the span points after an amount of spans equal to the frequency. This can be done by taking the remainder of the point divided by the frequency, via the remainder or modulo operation %. This must be done after calculating the base gradient values.

	public struct LatticeTiling : ILattice {

		public LatticeSpan4 GetLatticeSpan4 (float4 coordinates, int frequency) {
			coordinates *= frequency;
			float4 points = floor(coordinates);
			LatticeSpan4 span;
			span.p0 = (int4)points;
			span.p1 = span.p0 + 1;
			span.g0 = coordinates - span.p0;
			span.g1 = span.g0 - 1f;

			span.p0 %= frequency;
			span.p1 %= frequency;

			span.t = coordinates - points;
			span.t = span.t * span.t * span.t * (span.t * (span.t * 6f - 15f) + 10f);
			return span;
		}
	}

Now we can add tiling variants of all noise options that we currently support. Do this by alternating between the regular and tiling lattice versions in the array declaration of NoiseVisualization. I only show the change for regular Perlin noise.

		{
			Job<Lattice1D<LatticeNormal, Perlin>>.ScheduleParallel,
			Job<Lattice1D<LatticeTiling, Perlin>>.ScheduleParallel,
			Job<Lattice2D<LatticeNormal, Perlin>>.ScheduleParallel,
			Job<Lattice2D<LatticeTiling, Perlin>>.ScheduleParallel,
			Job<Lattice3D<LatticeNormal, Perlin>>.ScheduleParallel,
			Job<Lattice3D<LatticeTiling, Perlin>>.ScheduleParallel
		},

Instead of doubling the size of our dropdown enum we'll use a boolean toggle option to control tiling. The second array index them becomes equal to double the amount of dimensions, minus one if tiling is enabled and minus two otherwise.

	[SerializeField]
	bool tiling;
	
	…
	
	protected override void UpdateVisualization (
		NativeArray<float3x4> positions, int resolution, JobHandle handle
	) {
		noiseJobs[(int)type, 2 * dimensions - (tiling ? 1 : 2)](
			positions, noise, noiseSettings, domain, resolution, handle
		).Complete();
		noiseBuffer.SetData(noise);
	}

If we enable tiling at this point we get obvious repetition, if we increase the domain scale to see it, because a single tile fits inside a unit cube.

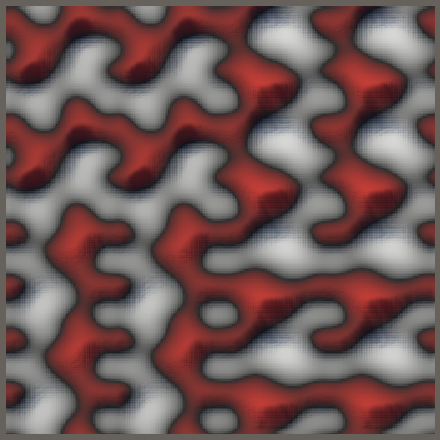
One octave frequency 2 tiling 2D Perlin; domain scale 4.

Although there is tiling it is incorrect, because the pattern depends on the sign of the dimension. 2D noise thus shows four different patterns. This happens because the remainder is influenced by the sign. To fix this we have to adjust LatticeTiling.GetLatticeSpan4.

Begin by checking whether the first point is negative after calculating its remainder. If so, we are on the wrong side, which we can fix by adding the frequency to the point.

			span.p0 %= frequency;
			span.p0 = select(span.p0, span.p0 + frequency, span.p0 < 0);
			span.p1 %= frequency;

We have to fix the second point as well. As it it always one step further in the positive direction than the first point, we can do this by basing it on the tiled first point instead of the untiled one.

			//span.p1 = span.p0 + 1;
			span.g0 = coordinates - span.p0;
			span.g1 = span.g0 - 1f;

			span.p0 %= frequency;
			span.p0 = select(span.p0, span.p0 + frequency, span.p0 < 0);
			span.p1 = (span.p0 + 1) % frequency;

3 octaves — Correct tiling, one and three octaves.

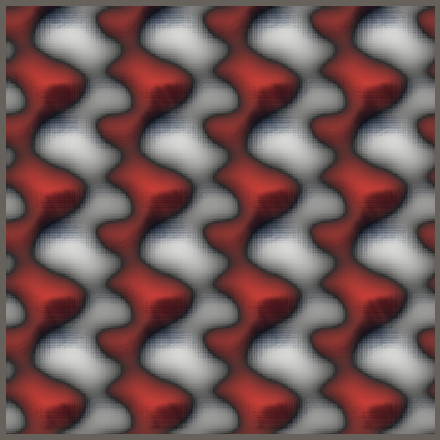
Once again, the main use for tiling noise is to create textures or meshes that can be seamlessly tiled. It can also be used to create looping 2D animations, by sampling multiple 2D slices of 3D noise.

Four times the same noise sample, domain scale 1.

Vectorized Tiling

Calculation of the integer remainder is done via integer division, which doesn't vectorize. As a result the tiling noise variants have to demultiplex the points, calculate the remainder per individual point, and then multiplex them again, which is inefficient. But this is not necessary.

Let's consider the second point of the span. We do not have to calculate the remainder for this point at all. We can get the same result by adding one to the first point and then checking whether it's equal to the frequency. If so, we're at the point where we have to repeat the pattern. As the pattern always starts at zero that's what the second point becomes.

			//span.p1 = (span.p0 + 1) % frequency;
			span.p1 = span.p0 + 1;
			span.p1 = select(span.p1, 0, span.p1 == frequency);

We do have to calculate the remainder of the first point, but we can do so via a floating-point division which does vectorize, by delaying the conversion to integer. The remainder is found by taking the original floored coordinate from before conversion to integer, dividing it by the frequency, then casting to integer, multiplying with the frequency, and subtracting that from the untiled first point.

			//span.p0 %= frequency;
			span.p0 -= (int4)(points / frequency) * frequency;
			span.p0 = select(span.p0, span.p0 + frequency, span.p0 < 0);

Directly converting the result of the floating-point division—in reality a multiplication with the reciprocal of the frequency—to an integer is dangerous, due to floating-point precision issues and rounding behavior. In this case we can round up the division before converting it, which we do via the ceil method. This ensures that it works correctly on all CPU types.

			span.p0 -= (int4)ceil(points / frequency) * frequency;

The next tutorial is Voronoi Noise.

license repository PDF